Volume of liquid flowing into a tank

[Ocis]

[SOLVED] Volume of liquid flowing into a tank

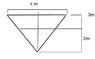
A tank in the shape of an inverted cone has liquid flowing into it at constant rate.
If the rate at which the water rises in the tank is 3x10^-2 m s^-1 when the liquid is at a depth of 2 m, calculate the volume of liquid flowing into the tank at m^3 s^-1.

The cone has a maximum diameter of 4 m and height 3m.

i know that the vol. of a cone = $$\frac{\Pi r^{2}h}{3}$$
I think this involves the volumes of revolution, where I have $$dy$$ as the thickness which would be $$3 X 10^{-2} m s^{-1}$$ at a vol. of 2 m in height and then I have an integral of the area and limits of height. But because it's a rate i must need to differentiate it whereby $$dv/dt = vol. m^{3} s^{-1}$$?

Any clues would be appreciated, thanks.

 

[Dick]

You don't need to integrate anything. Figure out the volume of liquid in the tank when the liquid is filled to height h. Notice this will require you to find r for the surface of the liquid at height h, you can't just use the 4 m diameter.

 

[konthelion]

Hint: Use similar triangles. The bigger triangle is the height and radius of the cone, and the smaller triangle: r and h. As a result, you can express the volume V in terms of h alone.

 

[Ocis]

Could I just use trig to work out the new radius
$$tan \Theta = {\frac{3}{2}} = 56.31$$

$${\frac{2}{tan 56.31}} = 1.34 (r)$$

$$Vol = {\frac{\Pi X 1.34^{2} X 2}{3}} = 3.72 m^{3}$$

But then how do I involve the flow rate which at that height 2m is $$3 X 10^{-2} m s^{-1}$$

 

[Vid]

You have V = pi/3r^2h. This means V is a function of two variables. You want to write r in terms of h so that you only have a function of one variable. The rate the water is rising is the change in height. How would you relate the change in height to get the change in volume using what you know?

 

[konthelion]

Could I just use trig to work out the new radius
$$tan \Theta = {\frac{3}{2}} = 56.31$$

$${\frac{2}{tan 56.31}} = 1.34 (r)$$

$$Vol = {\frac{\Pi X 1.34^{2} X 2}{3}} = 3.72 m^{3}$$

But then how do I involve the flow rate which at that height 2m is $$3 X 10^{-2} m s^{-1}$$

No, you can not use trig to solve in terms of r because this is a related rates problem; r is dependent upon h.

If you differentiate V with respect to t.
$$\frac{dV}{dt}=\frac{dV}{dh} \frac{dh}{dt}$$ where dV/dt=rate that the water is flowing into the cone, and dh/dt = rate that the water level is rising with respect to the height of the cone, dV/dh is the derivate of the volume V in terms of h. Now find r in terms of h first.

 

[Ocis]

Ok so how is this?
$$Volume = {\frac{\Pi X ({\frac{2}{3}}h)^{2} X h}{3}} ??$$
Then...?

 

[Dick]

Very nice. Now find dV/dt.

 

[Ocis]

Regrettably I am confused, again.. If I differentiate that volume I am getting
$${\frac{dv}{dh}}$$ ?? = $${\frac{4}{9}} h$$ then $${\frac{dv}{dt}}$$ = ? $${\frac{dv}{dh}}$$ x $${\frac{dh}{dt}}$$ where $${\frac{dh}{dt}}$$ = ( $$3$$ x $$10^{-2} ms^{-1}$$ ) ??

 

[Vid]

Don't worry about dv/dh. You don't need that. Just differentiate both sides of the volume equation with respect to t.

 

[Dick]

Regrettably I am confused, again.. If I differentiate that volume I am getting
$${\frac{dv}{dh}}$$ ?? = $${\frac{4}{9}} h$$ then $${\frac{dv}{dt}}$$ = ? $${\frac{dv}{dh}}$$ x $${\frac{dh}{dt}}$$ where $${\frac{dh}{dt}}$$ = ( $$3$$ x $$10^{-2} ms^{-1}$$ ) ??

Your dV/dh is way off. V=pi*(2h/3)^2*h/3. Maybe try and simplify that before you differentiate?

 

[Ocis]

Now I am even more confused... How do I differentiate both sides of the volume equation with respect to t ?

 

[Vid]

Implicit differentiation.

V = pi/3(2/3h)^2*h
dV/dt = (pi/3(2/3h)^2*h)' * dh/dt

Take the derivative and plug in the values you know. h = 2m. dh/dt is the change in the water level.

 

[Ocis]

Your dV/dh is way off. V=pi*(2h/3)^2*h/3. Maybe try and simplify that before you differentiate?

Ok, so am I wrong to think that constants such as Pi get canceled out and then everything else just individually divided by three (2/3h^2 / 3) (* h/3 )' which should = 4/27h ??

Sorry about this...

 

[Dick]

Ok, so am I wrong to think that constants such as Pi get canceled out and then everything else just individually divided by three (2/3h^2 / 3) (* h/3 )' which should = 4/27h ??

Sorry about this...

S'ok. You just aren't differentiating correctly. Multiplicative constants don't just 'cancel out'. And as you've written the expression you have two different factors depending on h, you would need the product rule. I suggest you review basic differentiation. While you're doing that rewrite V by combining the h's and numbers. Do you get pi*(4/27)*h^3? Now try differentiating wrt h again.

 

[Ocis]

Ok I get it all now very silly mistakes indeed. So using the product rule is it anything close to
$${\frac{4}{27}} h^{3} + {\Pi}{\frac{12}{27}}h^{2}$$

 

[Dick]

The silly mistakes aren't quite over. Where did you get the first term? What's the derivative of pi?

 

[Ocis]

Well obviously not 1? I have never differentiated pi before...? Or it is a constant and it should therefore cancel out the first part of the product rule because it equals 0 U'V leaving just $${\Pi}{\frac{12}{27}}h^{2}$$ ??

 

[Dick]

Well obviously not 1? I have never differentiated pi before...? Or it is a constant and it should therefore cancel out the first part of the product rule because it equals 0 U'V leaving just $${\Pi}{\frac{12}{27}}h^{2}$$ ??

Yes, exactly, it's just a constant like 4 or 27.