songoku
- 2,508
- 402
- Homework Statement
- A solid cylinder of radius r and height h is cut by a plane which passes through a diameter of the base and intersects the cylinder's top in just one point, cutting the cylinder into two parts. Calculate the volume of the smaller part
- Relevant Equations
- Integration
I imagine the shape will be like this:
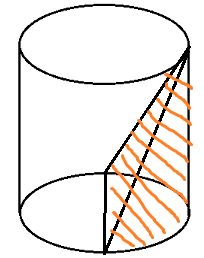
and I need to find the volume of the shaded part. I am planning to use: ##V=\int A(y) dy##
I tried to take the cross-sectional area A(y) to be triangle:
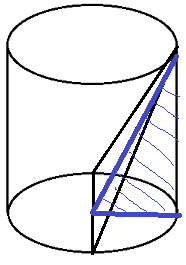
and the base of the cylinder to be:
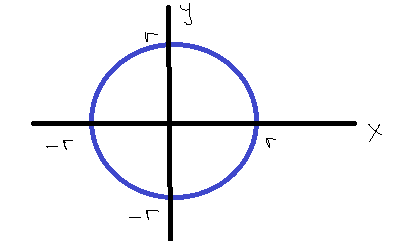
So it means that the base of the triangle will fulfill the equation of circle ##x^2+y^2=r^2## and the base will be ##x=\sqrt{r^2-y^2}##.
But I can't find the equation for the height of triangle. I imagine that the height will satisfy maybe equation of tilted parabola and I don't know how to find it.
Is my approach correct? Or maybe there is better method to do this question?
Thanks
and I need to find the volume of the shaded part. I am planning to use: ##V=\int A(y) dy##
I tried to take the cross-sectional area A(y) to be triangle:
and the base of the cylinder to be:
So it means that the base of the triangle will fulfill the equation of circle ##x^2+y^2=r^2## and the base will be ##x=\sqrt{r^2-y^2}##.
But I can't find the equation for the height of triangle. I imagine that the height will satisfy maybe equation of tilted parabola and I don't know how to find it.
Is my approach correct? Or maybe there is better method to do this question?
Thanks