Volumes of Solids of Revolution using Shells

[ineedhelpnow]

my final is tomorrow and my instructor gave a list of questions that will be similar to the ones on the final exam and i want to see how they should be done properly. I've been working on other problems but i can't get past these ones. thanks

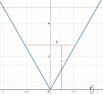
determine the volume using the shell method $y=5|x|$ about $y=5$ about the x-axis.

determine the volume using the shell method about the y-axis. $y=x^2$, $y=3+2x$, for $x \ge 0$

can you please show me how to do them step by step?

 

[MarkFL]

Let's look at the first one...here is a plot of the region to be revolved:

View attachment 2878

Now, let's compute the volume of an arbitrary shell...given by:

$$dV=2\pi rh\,dy$$

We need to express $r$ and $h$ in terms of $y$. What would you say these are?

 

[ineedhelpnow]

im not sure. is the height 5|x|-5? or something like that?

 

[Deveno]

$h$ runs between two different curves:

$y = 5x$ and

$y = -5x$

Since we are integrating with respect to $y$, we are going to want to express $x$ as a function of $y$ (we need to split the function:

$y = 5|x|$ into it's two "parts" because it's not one-to-one).

Thus we have two functions:

$x = f_1(y) = -\dfrac{y}{5}$, and:

$x = f_2(y) = \dfrac{y}{5}$.

Our distance $h$ is going to be $\sqrt{(x_2-x_1)^2 - (y_2-y_1)^2}$

where $x_2 = f_2(y_2)$ and $x_1 = f_1(y_1)$.

Since $h$ lies on the horizontal line going through $(0,y)$ we're going to have $y_2 = y_1$

so the $(y_2 - y_1)^2$ part of our distance formula is just going to be 0.

That means we just need to calculate $|x_2 - x_1|$, using our two formulas for the $x$'s.

 

[ineedhelpnow]

oh i just saw this reply. so the height is $\frac{2y}{5}$?

 

[Deveno]

That's a good start, now what's the radius?

 

[ineedhelpnow]

that's the thing. i can figure out the high normally but i also have trouble figuring out the radius.

 

[Deveno]

Look closer at Mark's picture.

 

[ineedhelpnow]

5-x?

 

[ineedhelpnow]

oh its in terms of y. never mind.

 

[Deveno]

Well, your original problem statement isn't all *that* clear about the axis of rotation, but let's say it's the $x$-axis.

The solid of revolution itself is going to look like a saucer with two shallow conical "hollows" or bores centered in it (in cross-section, it'll look like a bow-tie).

The "typical shell" we are using is the cylinder whose "edge" is the red line marked $h$ in Mark's drawing. Conveniently enough, the distance of this shell from the axis of revolution is ALSO the radius of the cylinder.

We are imagining this cylinder has "infinitesimal thickness" of $dy$. So the VOLUME element is this "tiny thickness" times the surface AREA of the cylinder.

Now the formula for the surface area of a cylinder is: $2\pi rh$.

This means $dV = 2\pi rh\ dy$

Isn't the shell whose outer edge is $y$ units away from the $x$-axis one with a radius of $y$?

Try to imagine this is a drawing of a REAL thing, perhaps something to be machined on a lathe. How would you measure the radius?

 

[ineedhelpnow]

sorry i meant AND y=5 not about y=5.

doesnt matter anymore though. already took the test. thanks for the previous posts though Deveno. they were very helpful :)

 

[Deveno]

sorry i meant AND y=5 not about y=5.

doesnt matter anymore though. already took the test. thanks for the previous posts though Deveno. they were very helpful :)

Well, I hope you did well. But I'd like to add that taking a course isn't really about the grade you get (it is only human nature to want to do well, of course). It's to acquire the knowledge. And while knowledge for just its own sake is still worthwhile, it's even more meaningful to USE it.

So it always matters. Hopefully, someone somewhere will read this thread, and think to themselves: oh, THAT'S how you do it.

You know, it's not the grade, or even the diploma that matters. It's what sticks. The only thing any of us here at MHB do is try to help that happen. When you KNOW a subject, when you own it, like knowing how to ride a bicycle, it's yours forever. Such things are precious beyond measure, and hard to quantify objectively.

 

[ineedhelpnow]

Well, I hope you did well. But I'd like to add that taking a course isn't really about the grade you get (it is only human nature to want to do well, of course). It's to acquire the knowledge. And while knowledge for just its own sake is still worthwhile, it's even more meaningful to USE it.

So it always matters. Hopefully, someone somewhere will read this thread, and think to themselves: oh, THAT'S how you do it.

You know, it's not the grade, or even the diploma that matters. It's what sticks. The only thing any of us here at MHB is try to help that happen. When you KNOW a subject, when you own it, like knowing how to ride a bicycle, it's yours forever. Such things are precious beyond measure, and hard to quantify objectively.

I think I've acquired knowledge and hopefully I am prepared for calculus 3 next semester. thanks