Volumetric flow rate ratio calculation

[Dario56]

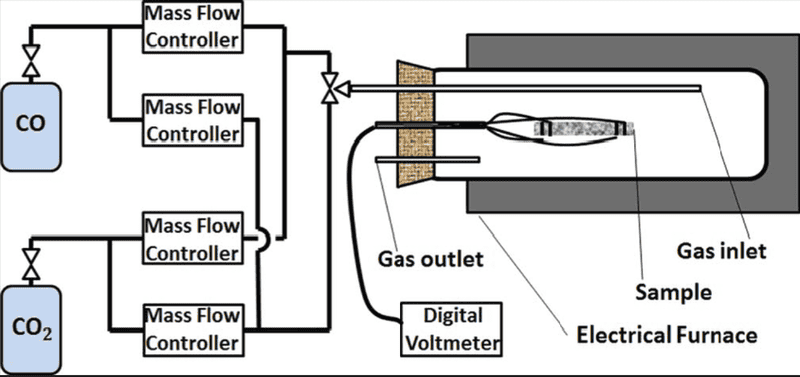
I'm using two tanks of nitrogen and oxygen and mixing them in different ratios to change the oxygen partial pressure in the system. System is opened to the atmosphere through the venting pipe which therefore sets the total pressure of the system to 1 bar. System is opened and gases flow through it. Schematic is provided to give better insight:

To create atmospheric composition of the mixture, mole fraction of oxygen needs to be 0.21 while nitrogen needs to be 0.79. Therefore, molar flow rate ratio, $A$ is: $$A = \frac {\dot n(O_2)}{\dot n(N_2)} = \frac {0.21}{0.79} = 0.266$$

Gas tanks are equipped with volumetric flowmeters. Relating volumetric and molar flow rates can easily be done if the assumption of ideal gas is valid. Since I'm using air at atmospheric pressure and high temperatures (500 – 800 $^\circ C$), the assumption should hold.

Volumetric flow ratio is: $$ \frac {\dot V(0_2)}{\dot V(N_2)} = \frac {\frac {\dot n(O_2)RT}{P(O_2)}} {\frac {\dot n(N_2)RT}{P(N_2)}} = A \frac {P(N_2)}{P(O_2)}$$

Since we're talking about the ideal gas, Dalton's law holds. Partial pressure ratio is equal to the mole fraction ratio of the components in the mixture. Therefore: $$\frac {P(N_2)}{P(O_2)} = \frac {1}{A}$$

Leading to the volumetric flow rate ratio being always equal to 1. This doesn't seem correct, what am I doing wrong?

 

[BvU]

Aren't the pressures in $$\frac {\dot V(0_2)}{\dot V(N_2)} = \frac {\frac {\dot n(O_2)RT}{P(O_2)}} {\frac {\dot n(N_2)RT}{P(N_2)}} = A \frac {P(N_2)}{P(O_2)}$$ and in $$\frac {P(N_2)}{P(O_2)} = \frac {1}{A}$$ different ?

$\$