Von Mises stress and real failures: Triaxial tension

[Juanda]

TL;DR Summary

Von Mises predicts triaxial compression/tension should not be problematic. In reality, triaxial tension does break the components.

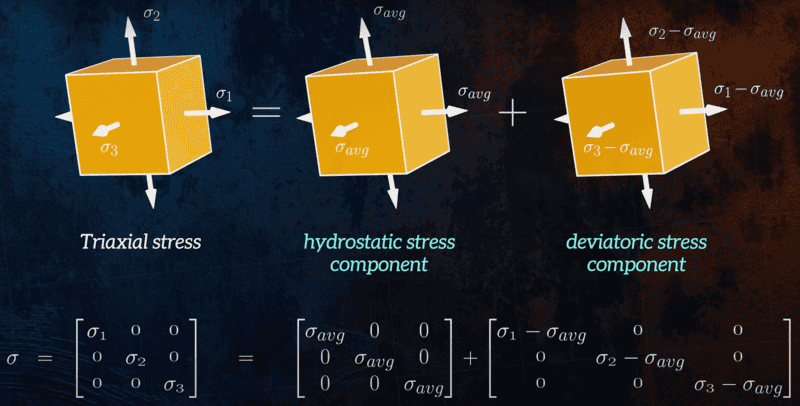
In broad terms, Von Misses is a failure theory that uses deviatoric stress to check if a ductile material will yield.

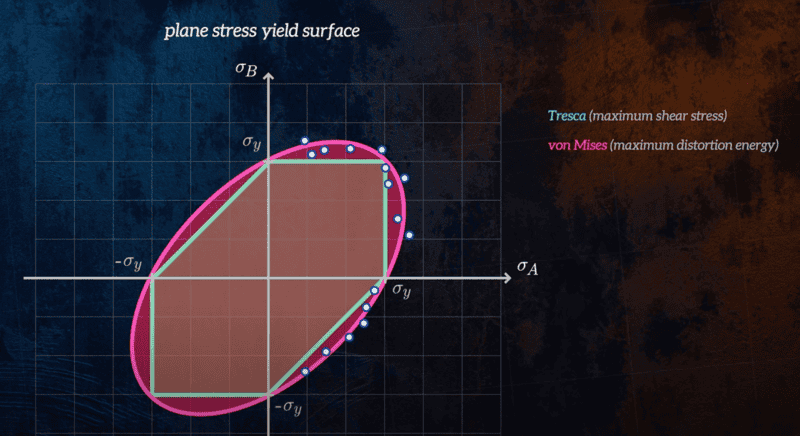
It's a fairly accurate failure theory because experimental results agree with the predicted results.

Extending the previous picture to 3D means that as long as the stress components are within the extruded cylinder, the material should not yield.

This has been proven to be true in triaxial compression. At least as far as the testing equipment can push the tested body.
However, in triaxial traction, the ductile material suffers a brittle fracture which is inconsistent with Von Mises's predictions.

I first learned about this when talking about welded components. In fact, I initially believed the explanation for this phenomenon was related to the rapid cooling associated with welds so the ductile material changes to brittle material in that area. But it is apparently a phenomenon that goes beyond that and can be observed in bodies without any weld.
The reason it shows in welds I believe is more related to the cooling of the cords that causes triaxial compression depending on their geometry. More information can be found here (link).

@berkeman please can you post the original message #7 that is now hidden from the original thread (link) for added context? It contained all the references necessary to better understand what I'm trying to describe.

So with all the context now exposed. Is there an explanation to predict the brittle fracture of ductile materials due to triaxial compression? All I could find are some recommendations based on experimentation to prevent loading components beyond that identified critical pressure.

 

[Juanda]

@berkeman please can you post the original message #7 that is now hidden from the original thread (link) for added context? It contained all the references necessary to better understand what I'm trying to describe.

I got temporary access to the hidden message #7. This is the content:

The documentation I could find this time is only available in Spanish. It's from Valladolid University (Universidad de Valladolid). The relevant part is chapter 3 (Elastic Solid) which talks about historical tests (traction and torsion), the generalized Hooke's Law, failure theories, etc. I'll try to translate and process the key bits most relevant to this conversation.

From page 35

Finally, notice that the experiences from Bridgman cannot be extrapolated to the triaxial traction. Although for triaxial compression the component could survive pressures as high as the equipment would allow, when the experiment is done with triaxial traction on "sweet steel" (acero dulce, carbon below 2%) a fragile fracture may happen at tensions higher than the elastic limit.

So the behavior predicted by Von Misses, an accurate and well-accepted theory for these materials, in the triaxial traction case differs from the experimental results. It makes sense we can't infinitely traction the part when pulling from all sides simultaneously but the change in behavior (fragile fracture in ductile material) baffles me.

From page 37

In the quadrant where all tensions are traction, it's not valid to think the plastification surface can be extended indefinitely. As it was previously pointed out, a fragile fracture will happen.

So the plastification surface predicted by the theory (what's shown is for Tresca, Von Misses would be a cylinder) must be capped somehow to agree with experimental results. I don't know if that cap can be derived mathematically or if it's obtained experimentally. The document shows the shape later.

From pages 40 and 41

To finish, let's revisit the possiblity of a fragile fractule of a normally ductile material when working in a triaxial traction state. Let's define a fracture surface as the geometrical place where the main tensions $\sigma_{I}$, $\sigma_{II}$ and $\sigma_{III}$ would cause the fracture of the material. If the fracture surface were reprensented overlapped with the plastification surface the result would be similar to what's shown in Figure 3.15a in which can be seen how fracture can happen inside the plastification surface. It is then possible to load the element is such way that it breaks before crossing the plastification surface. In other words, a fragile fracture.

The current version of the Techical Code for Edification (CTE: Código Ténico de la Edificación) does not mention this phenomemon. Perhaps because how unlikely it is to find building structures where triaxial traction occurs. However, such states can happen for example in welded joints due to residual stress depending on their geometrical disposition (as shown in this thread in the original post). Previous versions of the technical codes (EA95) indicated that even if Von Misses is satisfied it's also necessary to check $\sigma_{I}$<2$\sigma_{e}$.

I believe the red surface on the left picture is from experimental results. Then, on the right side, there's the engineering simplification to cap the predictions done by the Von Misses failure theory.

In conclusion, welding cords are just a scenario that makes triaxial traction more likely depending on how they are positioned. But it's not the reason behind the fragile fracture because such a phenomenon has been observed in cases where there are no welding cords involved.

It feels like there are two mechanisms at play to describe the behavior of a chunk of metal under load. Theories like linear elasticity + Von Misses in one of them and it predicts the results pretty well within certain limits ($\sigma_{I}$<2$\sigma_{e}$). But there is a point where the similarities with reality break apart and not by a little bit. According to Von Misses the chunk of metal can be loaded indefinitely and in reality, we see a fragile fracture. (We could say the theory breaks in both directions since if we keep compressing the component then nuclear things could start happening at some point but that's beyond practical applications and the intended purpose of this post)

This post kind of answers the original question.

Does the fabrication process of the 3 cords contacting each other change the chemical properties of the metal so it's no longer ductile? Is it that the high temperatures involved and rapid cooling make it fragile?

We now know that welding cords are not the origin of the phenomenon. However, it opens even more concerning/interesting questions. What's that second mechanism at play? Why does the change in behavior (ductile → fragile) happen in the shown scenario?

Anyway, that's all I could find for the moment. Just like with anything else, this is probably a well-studied and documented phenomenon with math already developed around it. If you know of it let me know, please.

 

[jrmichler]

Just like with anything else, this is probably a well-studied and documented phenomenon with math already developed around it. If you know of it let me know, please.

It has been studied by the structural steel industry because they had problems welding large sections.

I dug through my copy of Steel Structures, by Salmon and Johnson, Second Edition. Here is a quote: In general, welding creates a built-in continuity that gives rise to biaxial and triaxial stress and strain conditions, which result in brittle behavior. My hazy recollection is that this is a real problem when welding steel more than 4 inches thick. I remember reading about brittle fracture in large sections sometime in the 1990's, so look for sources newer than that book, which was published in 1980.

Searching on the AISC site (https://www.aisc.org) found a document titled Welding Heavy Structural Steel—Successfully. A quote from that document: High restraint is typically associated with welds with all of the following conditions: weld throat dimensions of 2 in. or greater, weld lengths of 11/2 ft or more, and where steel members intersect from all three orthogonal directions. High restraint in welded joints causes high triaxial tensile stresses, which cause brittle fracture and lamellar tearing.

I suggest searching the AISC site, then follow up the references you find there. Because the driving force behind this research was field problems, you may find that most information is more empirical than theoretical. If for no other reason, there are few research universities capable of welding and testing large structural steel structures.

 

[Juanda]

I dug through my copy of Steel Structures, by Salmon and Johnson, Second Edition. Here is a quote: In general, welding creates a built-in continuity that gives rise to biaxial and triaxial stress and strain conditions, which result in brittle behavior. My hazy recollection is that this is a real problem when welding steel more than 4 inches thick. I remember reading about brittle fracture in large sections sometime in the 1990's, so look for sources newer than that book, which was published in 1980.

The first time I came across this phenomenon was with someone talking to me about ships in WW2 suffering brittle fractures on the welded ribs so that would set the date a little further back than the 1980's.
However, I'm not certain if that's anectodical or just an urban legend. A while back I found a related article that indicated the brittle behavior of those metal sheets was due to the low temperature of the water so maybe this person that told me about it just got things mixed in his head or didn't fully understand what he was talking about.
https://www.revistac2.com/el-extrano-caso-del-metal-que-no-soportaba-el-frio/

Liberty S.S. Schenectady 1943

I'll keep trying to find more related information about this. Your suggestion for sources and dates sets a good initial point to start looking for.
I'll post it back here if I come across something that is interesting.

 

[Juanda]

It has been studied by the structural steel industry because they had problems welding large sections.

I dug through my copy of Steel Structures, by Salmon and Johnson, Second Edition. Here is a quote: In general, welding creates a built-in continuity that gives rise to biaxial and triaxial stress and strain conditions, which result in brittle behavior. My hazy recollection is that this is a real problem when welding steel more than 4 inches thick. I remember reading about brittle fracture in large sections sometime in the 1990's, so look for sources newer than that book, which was published in 1980.

Searching on the AISC site (https://www.aisc.org) found a document titled Welding Heavy Structural Steel—Successfully. A quote from that document: High restraint is typically associated with welds with all of the following conditions: weld throat dimensions of 2 in. or greater, weld lengths of 11/2 ft or more, and where steel members intersect from all three orthogonal directions. High restraint in welded joints causes high triaxial tensile stresses, which cause brittle fracture and lamellar tearing.

I suggest searching the AISC site, then follow up the references you find there. Because the driving force behind this research was field problems, you may find that most information is more empirical than theoretical. If for no other reason, there are few research universities capable of welding and testing large structural steel structures.

I found this document in the AISC site and it is from 1995.
Structural Details to Increase Ductility of Connections. It can be found on the internet too but I can't upload it because it says the PDF is too heavy. Can I even share the paper here? https://www.aisc.org/products/engin...details-to-increase-ductility-of-connections/

I'm finding the document a little hard to digest but it's definitely related to what we are discussing here.
By the way, again, the anecdotes from shipyards during WW2 come into play.

The paper describes two failure modes. Yielding is related to shear stress and fracture which is related to the critical tensile stress.

I guess Von Mises works well with the yielding failure mode but not so much with the brittle fracture.

My current intuition is that shear stress causes the crystallographic planes to slide over one another if it's big enough resulting in plastic deformation which is the tipical behaviour of ductile metals. However, in triaxial tension, the planes cannot slide because they're being pulled from all sides. At some point the electrical forces keeping the metal together like little springs are not strong enough and it simply snaps coming apart.
This is just a handwavy explanation of what's going on. I'd like to better understand the mechanisms at play. For example, it does not explain why in the tensile specimens end up breaking. I guess at some point the crystallographic planes cannot slide so easly because of the accumulation of errors in the crystal mesh (cold hardening due to necking) and once it's locked in place increasing the tension will result in the specimen breaking in two when, again, the electric forces cannot hold the part together any longer.