Waiting time in a Queue using Poisson arrival

[Mehmood_Yasir]

Hi. My apologizes for bothering your again. I spent a lot of time to figure out the reason for discrepancies between sim and ana results for lower values of lambda, while calculating the expected waited time of the second arrival. Unfortunately, its still the same discrepencies for lower values of lambda.
I attached figure. I tried for every way by seeing the possible logic. I kept k=1 (expected time for wanting 1 arrival) and K=2 (expected time for wanting 2 arrivals) and the difference gives the expected time associated for wanting a second arrival. Later, I subtracted the difference from the max. waiting time of first arrival. The outcomes are below. Still not good (magenta and blue curves).

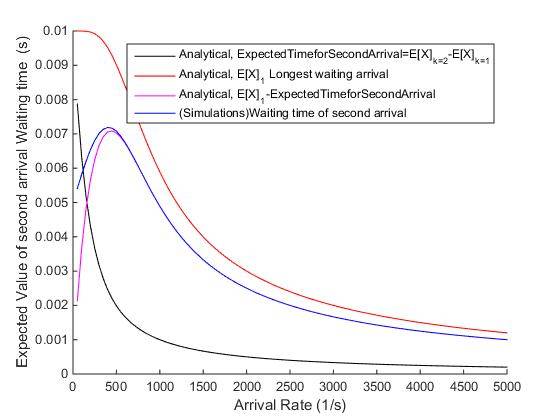
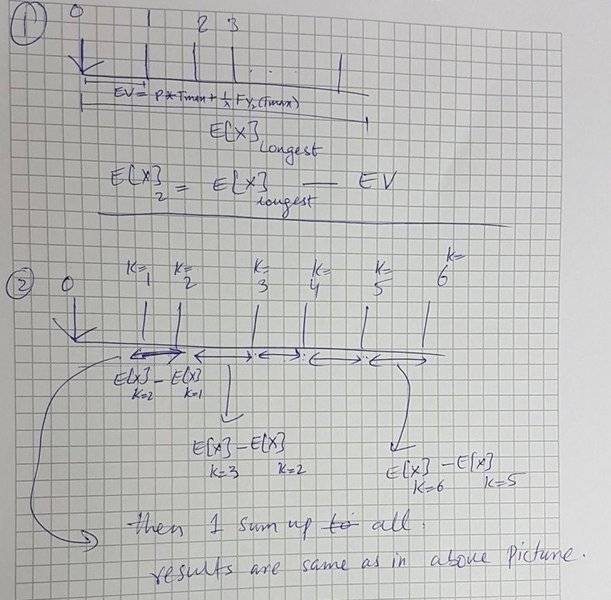
I used another way to find out this delay as shown in the below picture in (2) outcomes are still same.

 

[StoneTemplePython]

Let me try to recap this. You originally asked one and only one question and this was answered many different ways.

You then proceeded two ask two new questions, for which you already have asymptotically correct answer(s).

With respect to your second question, you’ve made statements like “For the second question, what I wanted to find is the average waiting time of an aggregated packet due to k arrivals. ”. There are some major subtleties related to conditioning here, but literally interpreted, with respect to your question, I’d point out:

On page 1 of this thread I mentioned chapter two of:
https://ocw.mit.edu/courses/electri...tochastic-processes-spring-2011/course-notes/

The literally interpreted second question is directly addressed in the notes. The fact is that if you condition on the total number of arrivals at some time period $\tau$, you get a uniform distribution between the arrivals. This has the key to your second question. You’ve said you studied these notes. Did you do any of the exercises at the end? If so, how many? I am getting the feeling that you want answers and don’t want to put in the work.

In summary I have 3 major concerns. (1) There is considerable mission creep going on in this thread. (2) There are serious subtleties related to conditioning that I’m not convinced you appreciate. (3) It’s feeling like you aren’t interested in learning and just want someone else to solve your problems for you.

If you put in the work and solve a majority of those chapter 2 exercises or complete 6.041x, I may change my mind. Otherwise I have little further interest in this thread.

 

[Mehmood_Yasir]

Dear friend, Thanks a lot for your kind advice and help, as well as time.
Its correct I did not solve the exercises given in the notes. But, I read the early part of notes even before this thread. Based on your advice, I revisited again the notes. Thanks for the advice. The good news is for the above figure where I plotted the mistmatch b/w analytical and simulation for the waiting time of the second segment is corrected now. The only issue was that in our case, the expectation value until getting another arrival must be also conditioned for $X<= T_{max}$ as in our case the expectation value cannot exceed $T_{max}$, I recalculated the expectation value with this conditioning and used for calculating the expected waiting time for the second segment.