Want to understand how to express the derivative as a matrix

[nomadreid]

TL;DR

In the brief article cited in the description, the author gives a very limited example of how to interpret the derivative as a matrix. It is unclear how to extend this example to more general cases.

In https://www.math.drexel.edu/~tolya/derivative, the author selects a domain P_2 = the set of all coefficients (a,b,c) (I'm writing horizontally instead off vertically) of second degree polynomials ax^2+bx+c, then defines the operator as matrix

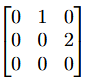
to correspond to the d/dx linear transformation. (We are not dealing with partial derivatives, etc.)

The author then continues with the domain of P_n = the set of all coefficients of n-degree polynomials, and the corresponding (n+1)x(n+1) matrix is defined analogously.

So, the author has defined matrices that correspond to the simple derivative for polynomials in one variable. However, I don't see how you could extend this to functions (of one variable) expressed with non-positive integer exponents. Can one, or does one have to take another tack? If the latter, which?

Motivation for my question: it is said that every linear transformation corresponds to a matrix; since d/dx is a linear transformation, there must be a matrix for it, but .... which?

Thanks in advance.

 

[martinbn]

You need to specify the space you consider. If it is not the space of polynomials of degrees up to $n$, then which one do you want?

 

[scottdave]

Derivative of a polynomial is pretty easy, so the matrix should be fairly easy to determine, especially when the powers of x are positive integers.

Note that it should be a + b*x + c*x^2 for this matrix to work properly. That is how the paper frames the polynomial coefficients.

 

[nomadreid]

You need to specify the space you consider. If it is not the space of polynomials of degrees up to $n$, then which one do you want?

Thanks, martinbn. I would like all differentiable functions, but perhaps the key is that all functions differentiable at a point can be expressed as a polynomial, even though it might be infinite (i.e., infinite series), so therefore this method leads us to being able to include all differentiable functions assuming we allow infinite matrices? Floating a lead balloon here....

Derivative of a polynomial is pretty easy, so the matrix should be fairly easy to determine, especially when the powers of x are positive integers.

Note that it should be a + b*x + c*x^2 for this matrix to work properly. That is how the paper frames the polynomial coefficients.

Thanks, scottdave, for pointing that out.

 

[pasmith]

Motivation for my question: it is said that every linear transformation corresponds to a matrix; since d/dx is a linear transformation, there must be a matrix for it, but .... which?

The matrix representation of a linear map depends on the choice of basis. In your example of polynomials of degree at most 2, taking the basis as the first three Chebyshev polynomials will give a different representation of the derivative than taking \{1, x, x^2\}. Or given any three distinct points in [a,b] we could take the Lagrange interpolating polynomials for those points as our basis, and the derivative matrix would again be different.

Thanks, martinbn. I would like all differentiable functions, but perhaps the key is that all functions differentiable at a point can be expressed as a polynomial, even though it might be infinite (i.e., infinite series), so therefore this method leads us to being able to include all differentiable functions assuming we allow infinite matrices?

The functions you are looking for are those which are analytic at a point, ie. they have a Taylor series centered at that point which converges to the function in some open neighbourhood of it.

Functions which are merely smooth may not have a convergent Taylor series, for example <br /> f: x \mapsto \begin{cases} 0 &amp; x= 0 \\ e^{-1/x^2} &amp; x \neq 0 \end{cases} where all derivatives exist and are zero at the origin, but f(x) \neq 0 for x \neq 0.

 

[nomadreid]

The matrix representation of a linear map depends on the choice of basis. In your example of polynomials of degree at most 2, taking the basis as the first three Chebyshev polynomials will give a different representation of the derivative than taking \{1, x, x^2\}. Or given any three distinct points in [a,b] we could take the Lagrange interpolating polynomials for those points as our basis, and the derivative matrix would again be different.
The functions you are looking for are those which are analytic at a point, ie. they have a Taylor series centered at that point which converges to the function in some open neighbourhood of it.

Functions which are merely smooth may not have a convergent Taylor series, for example <br /> f: x \mapsto \begin{cases} 0 &amp; x= 0 \\ e^{-1/x^2} &amp; x \neq 0 \end{cases} where all derivatives exist and are zero at the origin, but f(x) \neq 0 for x \neq 0.

So, it appears that I am back to square one on the (modified) motivating goal that I started with, given a vector space V, a specific basis, and a linear transformation T on V, there is a matrix that corresponds to T.

Given your excellent point about the existence of linear transformations without convergent Taylor series, it would appear that extending the method given in the cited article is doomed to failure. Although it could work if I substituted "analytic function" for "linear transformation", this does not go far enough for the more general statement of the cited goal.

That does not rule out the existence of another means to prove the existence of a matrix (for a given basis) for every linear transformation, but I have not found it (although I have often found the assertion) on the Internet. Further clues? (With thanks for those given so far.)

 

[fresh_42]

TL;DR Summary: In the brief article cited in the description, the author gives a very limited example of how to interpret the derivative as a matrix. It is unclear how to extend this example to more general cases.

Can one, or does one have to take another tack? If the latter, which?

I wrote 5 articles about derivatives:
https://www.physicsforums.com/insights/the-pantheon-of-derivatives-i/
which I hoped to cover the subject and counted 10 interpretations of derivatives in
https://www.physicsforums.com/insights/journey-manifold-su2mathbbc-part/

If you only have numbers $a_{ij}$, as in the case of a matrix $A$, then you have derivatives of a function $f=(f_1,\ldots,f_m) \, : \, \mathbb{R}^n\longrightarrow \mathbb{R}^m$ which are evaluated at a certain point $p\in \mathbb{R}^n$
$$
a_{ij} = \left.\dfrac{\partial }{\partial x_i }\right|_{\boldsymbol x=p}f_j(\boldsymbol x)
$$

 

[pasmith]

I wrote 5 articles about derivatives:
https://www.physicsforums.com/insights/the-pantheon-of-derivatives-i/
which I hoped to cover the subject and counted 10 interpretations of derivatives in
https://www.physicsforums.com/insights/journey-manifold-su2mathbbc-part/

If you only have numbers $a_{ij}$, as in the case of a matrix $A$, then you have derivatives of a function $f=(f_1,\ldots,f_m) \, : \, \mathbb{R}^n\longrightarrow \mathbb{R}^m$ which are evaluated at a certain point $p\in \mathbb{R}^n$
$$
a_{ij} = \left.\dfrac{\partial }{\partial x_i }\right|_{\boldsymbol x=p}f_j(\boldsymbol x)
$$

I think here we are concerned with the derivative as a linear operator between function spaces, or finite-dimensional subspaces thereof.

 

[fresh_42]

I think here we are concerned with the derivative as a linear operator between function spaces, or finite-dimensional subspaces thereof.

Oh! Thanks for correcting me.

I can do that (only an example):

However, I don't see how you could extend this to functions (of one variable) expressed with non-positive integer exponents.

https://www.physicsforums.com/insights/journey-manifold-su2-part-ii/