- #1
Physicist1011
- 68
- 1
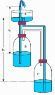
For a vertical pipe of water can the pipe length affect the velocity of the water?
note: the water is flowing through this vertical pipe.
note: the water is flowing through this vertical pipe.