How Do You Sketch the Solution of a Wave Equation with Given Initial Conditions?

[JI567]

Homework Statement

Ytt = 1 Yxx

with initial conditions of
yT(x,0) = 0
y(x,0) = $$

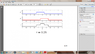
Sketch the solution of this wave equation for 5 representative values of t, when the solution of the wave is considered on the infinite domain

Homework Equations

D'alembert solution

$$ (f(x+ct)+f(x-ct)) + $$ $$

The Attempt at a Solution

As the g(x) part was 0 I tried solving it by
y(x,t) = φ1(x,t) + φ2(x,t)

where φ1 = $$ f(x+ct) and φ2 = $$ f(x-ct)

but I am not sure how to sketch it, can somebody please help me?

The solution should look like this

 

[Orodruin]

You seem to be off to a good start with the shape of the wave for two given times. I would perhaps sketch it for one or two more times, but generally you are doing fine.

 

[JI567]

You seem to be off to a good start with the shape of the wave for two given times. I would perhaps sketch it for one or two more times, but generally you are doing fine.

The pictures were given in the solution and I need to sketch for 0.5 and 0.75s. I understand how it works for t=0 but can you please explain how did the wave get that shape for t = 0.25. Explain all three parts of the graph please.

 

[Orodruin]

How do the +-ct parts in the argument affect the shape of the solution for different times?

 

[Chestermiller]

The figure you showed illustrates what is happening very nicely and intuitively. Half the solution is moving to the right (the middle red plot) with velocity c = 1, and half the solution is moving to the left (I can't tell what color that curve is from the figure, but it's the upper plot) with velocity c = 1. The two portions of the solution sum to the full solution (the lower plot, which is the sum of the red plot and the other plot).

Chet

 

[JI567]

The figure you showed illustrates what is happening very nicely and intuitively. Half the solution is moving to the right (the middle red plot) with velocity c = 1, and half the solution is moving to the left (I can't tell what color that curve is from the figure, but it's the upper plot) with velocity c = 1. The two portions of the solution sum to the full solution (the lower plot, which is the sum of the red plot and the other plot).

Chet

The solution moving to left is blue part. Yeah I got that the lower black part is the sum of red and blue plot. But let's say when t = 0.25 and x = 1.5. The red part is the φ2 and the blue part is φ1. I get how both parts are mvoing due to +- ct to the left or right. But the lowest part why did it get split into different parts and why at x =1.5 is the highest part? why not in other points. Also just for the record the y(x,0) is actually 2 for 1<x <2 for this question so please ignore the value I posted in the question, its not letting me edit it there.

I have attached a better picture of the graph

 

[Chestermiller]

I'm really having trouble understanding what your issue (doubt) is. The red plus the blue equals the solution. The picture tells the whole story. You've already articulated all this.

Chet

 

[JI567]

I'm really having trouble understanding what your issue (doubt) is. The red plus the blue equals the solution. The picture tells the whole story. You've already articulated all this.

Chet

My issue is I didn't draw the graph in the picture! This picture was already given in the question but I need to know why is the lowest part drawn like that? I mean why is the maximum at x = 1.5 and then it gets split into two sides?

 

[Ray Vickson]

My issue is I didn't draw the graph in the picture! This picture was already given in the question but I need to know why is the lowest part drawn like that? I mean why is the maximum at x = 1.5 and then it gets split into two sides?

I think you need to actually DRAW the graph yourself, not just look at what somebody else has drawn. Your sketches can be "rough", but they need to be good enough to illustrate what is happening. Here are the steps:
(1) For your given value of t > 0, draw the graphs of y = f(x-ct) and y = f(x+ct).
(2) Add them up: the graph of y = f(x-ct) + f(x+ct) just adds together the y-values on each of the two separate graphs.

I am absolutely serious about the above advice: until you actually carry out the steps yourself you will remain confused and uncertain.

 

[Chestermiller]

My issue is I didn't draw the graph in the picture! This picture was already given in the question but I need to know why is the lowest part drawn like that? I mean why is the maximum at x = 1.5 and then it gets split into two sides?

It's the opposite. The upper two parts have to be summed to give the lower part (which is the solution). What do you get at x = 1.5 when you sum the upper two parts?

Chet

 

[JI567]

It's the opposite. The upper two parts have to be summed to give the lower part (which is the solution). What do you get at x = 1.5 when you sum the upper two parts?

Chet

i get y = 1.5 then...is that correct?

 

[Chestermiller]

i get y = 1.5 then...is that correct?

No. You can see from the figure that it's 2.0.

 

[JI567]

No. You can see from the figure that it's 2.0.

Okay so from 1.25<x<1.75 why is y 2? and why is it 1 for the remaining left and right sides?

 

[Chestermiller]

Okay so from 1.25<x<1.75 why is y 2?

A 1.0 is contributed by the red profile and another 1.0 is contributed by the blue profile.

and why is it 1 for the remaining left and right sides?

Do you understand that the red profile represents f(x-ct)/2, and the blue profile represents f(x+ct)/2. The initial red profile has moved 0.25 to the right by the time t = 0.25, and the initial blue profile has moved 0.25 to the left by the time t = 0.25.

Also, note that the solution goes to zero at time t = 0.25 for values of x >2.25 and x < 0.75. Do you see that?

Chet

 

[JI567]

A 1.0 is contributed by the red profile and another 1.0 is contributed by the blue profile.

Do you understand that the red profile represents f(x-ct)/2, and the blue profile represents f(x+ct)/2. The initial red profile has moved 0.25 to the right by the time t = 0.25, and the initial blue profile has moved 0.25 to the left by the time t = 0.25.

Also, note that the solution goes to zero at time t = 0.25 for values of x >2.25 and x < 0.75. Do you see that?

Chet

yeah I see that...well okay so why isn't here the lowest part 2 then? The red and blue are still cotributing 1 each

 

[Chestermiller]

Well, that's only at one instant of time at one isolated point. I guess at t = 0.5 there should be a dot at x = 1.5, y = 2. But, it's not worth including.

Chet

 

[JI567]

Well, that's only at one instant of time at one isolated point. I guess at t = 0.5 there should be a dot at x = 1.5, y = 2. But, it's not worth including.

Chet

what do you mean? What so special happened between t =0.25 and t = 0.5 that the y decreased to 1?

 

[Chestermiller]

what do you mean? What so special happened between t =0.25 and t = 0.5 that the y decreased to 1?

Nothing. The region of overlap between the red and the blue just decreased. Did you check out what happens after t =0.5?

 

[JI567]

Nothing. The region of overlap between the red and the blue just decreased. Did you check out what happens after t =0.5?

yeah I checked this is what happens in after t = 0.5

Can you please explain what steps should I do in order to draw these type of graphs for different t's...I am so confused

 

[Chestermiller]

You take half the initial y profile and move it to the right a distance ct to get the red profile. You again take half the initial y profile and move it to the left a distance ct to get the blue profile. Then you add the red and the blue profiles together to get the black profile.

 

[JI567]

Nothing. The region of overlap between the red and the blue just decreased. Did you check out what happens after t =0.5?

so what is this region of overlap? How am I supposed to identify these regions? Half the initial y is moving to the left by 0.5 and to the right by 0.5. But however they are not getting add up this time to get solution y and also how much distance ct is solution y moving by?

 

[Chestermiller]

so what is this region of overlap? How am I supposed to identify these regions? Half the initial y is moving to the left by 0.5 and to the right by 0.5. But however they are not getting add up this time to get solution y

In this particular problem, after t = 0.5, they are no longer overlapping.

and also how much distance ct is solution y moving by?

It's like one part of the solution is sliding to the right at the speed of c, and the other part of the solution is sliding to the left at the speed c. Think of the two parts of the solution as actually having velocity, each with the speed of c.

Chet

 

[JI567]

Okay so how would I understand if the left and right are not overlapping for another problem?

What's happening in t = 1...now why are there two separate parts in the y solution

In this particular problem, after t = 0.5, they are no longer overlapping.

It's like one part of the solution is sliding to the right at the speed of c, and the other part of the solution is sliding to the left at the speed c. Think of the two parts of the solution as actually having velocity, each with the speed of c.

Chet

 

[Chestermiller]

Okay so how would I understand if the left and right are not overlapping for another problem?

What's happening in t = 1...now why are there two separate parts in the y solution

I've run out of ideas on how to explain this all. This is my last try. From time zero, there are always two separate parts to the solution. One is moving to the left at speed c, and the other is moving to the right at speed c. At any time t, they add together to form the overall solution. Each part is half of the initial profile. In any other problem, you do the same thing. You split the initial profile into two equal parts, and send one of these to the left and the other to the right, each with the speed c. At any time t, you add them together to get the overall solution. If, in a given problem, the domain of the initial profile is non-zero in some finite region, then, after the two profiles no longer overlap, the subsequently remain separate.

Chet

 

[JI567]

I've run out of ideas on how to explain this all. This is my last try. From time zero, there are always two separate parts to the solution. One is moving to the left at speed c, and the other is moving to the right at speed c. At any time t, they add together to form the overall solution. Each part is half of the initial profile. In any other problem, you do the same thing. You split the initial profile into two equal parts, and send one of these to the left and the other to the right, each with the speed c. At any time t, you add them together to get the overall solution. If, in a given problem, the domain of the initial profile is non-zero in some finite region, then, after the two profiles no longer overlap, the subsequently remain separate.

Chet

Okay got it. Do you know how to program these type of graphs in MATLAB? I mean I know how to plot graphs in Matlab by writing programming codes but for these type of graphs do I just write the D'Alembert function?

 

[Ray Vickson]

Okay got it. Do you know how to program these type of graphs in MATLAB? I mean I know how to plot graphs in Matlab by writing programming codes but for these type of graphs do I just write the D'Alembert function?

Do it, and see what you get.

 

[JI567]

Do it, and see what you get.

Do what? I wrote the D'alembert function...I get error message on MATLAB? What do I do now?

 

[Ray Vickson]

Do what? I wrote the D'alembert function...I get error message on MATLAB? What do I do now?

I can't help, since I have no access to Matlab and do not know much about it.