Wave equation of string under tension with a mass at x(a)

[Dustinsfl]

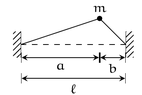
We have a string of length \(\ell\) with fixed end points. At \(x(a)\), we have a mass. We can break the string up into two sections \(a + b = \ell\); that is, a is the distance up to the mass and b afterwards. The string is under tension \(T\).
View attachment 3284
My question is why is the DE then
\[
m\ddot{x} + \Big(\frac{1}{a}+\frac{1}{b}\Big)Tx = 0
\]
Shouldn't this work out to be the wave equations?
Can someone explain where \(\big(\frac{1}{a}+\frac{1}{b}\big)\) this piece comes from?

 

[jvicens]

The equation \[
m\ddot{x} + \Big(\frac{1}{a}+\frac{1}{b}\Big)Tx = 0
\]
is not the wave equation, but rather the equation of motion for the mass on the string. This equation is derived from Newton's second law, which states that the sum of the forces acting on an object is equal to its mass times its acceleration.

In this case, the mass is subject to two forces: the tension in the string and the force of gravity. The tension in the string is given by the equation \(\frac{T}{a}x(a)+\frac{T}{b}x(b)\), which is the sum of the forces acting on the mass at points \(a\) and \(b\). This is divided by the mass \(m\) to get the acceleration term \(\Big(\frac{1}{a}+\frac{1}{b}\Big)Tx\).

To understand where the term \(\big(\frac{1}{a}+\frac{1}{b}\big)\) comes from, we can think about the physical interpretation of this equation. The term \(\frac{1}{a}\) represents the acceleration of the mass due to the tension at point \(a\), and \(\frac{1}{b}\) represents the acceleration due to the tension at point \(b\). Adding these two terms together gives the total acceleration of the mass on the string.

In summary, the equation \[
m\ddot{x} + \Big(\frac{1}{a}+\frac{1}{b}\Big)Tx = 0
\]
is derived from Newton's second law and represents the equation of motion for the mass on the string, not the wave equation. The term \(\big(\frac{1}{a}+\frac{1}{b}\big)\) represents the total acceleration of the mass due to the tension at points \(a\) and \(b\).