Wave function of infinite potential well

[keyzan]

Homework Statement

Determine the constant N from the normalization condition.

Relevant Equations

.

Hi guys i have this exercise:

A particle of mass m, confined in the segment -a/2 < x < a/2 by a one-dimensional infinite potential well, is in a state represented by the wave function:

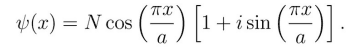1. Determine the constant N from the normalization condition.

To do this, I have to integral the square modulus of the function between minus infinity and plus infinity usually.. In this case however the integral diverges so I wonder. In cases like this can I restrict the integral in the area of zero potential (between -a/2 and a/2)? Also because only here the function is different from 0. I have already calculated this integral and I obtain that N^2 = 16/(5a). Can I accept this result?
---

 

[BvU]

can I restrict the integral in the area of zero potential (between -a/2 and a/2)

Definitely, yes !

I obtain that N^2 = 16/(5a)

You may want to check that...

$\$

 

[DrClaude]

To do this, I have to integral the square modulus of the function between minus infinity and plus infinity usually.. In this case however the integral diverges so I wonder. In cases like this can I restrict the integral in the area of zero potential (between -a/2 and a/2)?

The wave function is 0 outside the range $[-a/2,a/2]$, so the integral from $-\infty$ to $\infty$ cannot diverge.

 

[keyzan]

Thanks for the feedback. The second point reads:
2. Determine the possible outcomes of an energy measurement and the related probabilities

To do this I transformed the sines and cosines:

$\psi(x) = \sqrt{ \frac {8}{5a}} \frac {e^ { \frac {i \pi x}{a}} + e^ { -\frac {i \pi x}{a}}}{2} (1 + \frac {e^ { \frac {i \pi x}{a}} - e^ { -\frac {i \pi x}{a}}}{2})$

Multiplying the terms and then returning to writing sines and cosines I obtain:
$\psi(x) = \sqrt{ \frac {8}{5a}} cos(\frac {\pi x }{a}) + \sqrt{ \frac {8}{5a}} \frac {i}{2} sen(\frac {2 \pi x }{a})$
So psi is nothing more than a linear combination of the states with n=1 and n=2. Consequently we have only two energy outcomes:
$E_1 = \frac {\hbar^2 \pi^2} {2ma^2}$

and
$E_2 = \frac {4\hbar^2 \pi^2} {2ma^2}$
So to calculate the probabilities I have to calculate the square module of the two coefficients normalized to the sum of the two square modules. Everything is correct?

 

[hutchphd]

Sounds fine. And be sure the probabilities sum to 1 (as a double check) Any other sanity checks you can use? (I am terrible at Algebra and so I always search for reassuring checks and limits ... a good habit for the not-so-meticulous)

 

[keyzan]

Mmh.. The sum of the probabilities is different from 1.. So should I enter another normalization constant? (Initially I thought: I just calculated a normalization constant for this purpose!!!. But actually the previously calculated N should not normalize in the case in which we consider the probability of the energy outcomes but when we consider the outcomes of x. Or am I wrong? I'm a bit confused)


Edit 1: Waitt.. If the sum of the two square modules does not equal one then we just need to divide the square module of the coefficient of one of the two outcomes by the sum of the two square modules and then we normalize everything (without adding any other normalization constant). In case we want to normalize anyway, is it wrong to multiply psi by a new constant?

Anyway my results are:

$P(E_1) = \frac {4}{3}$
$P(E_2) = \frac {1}{3}$

Nice!

 

[kuruman]

For a symmetric infinite well of width $a$ $$E_n = \frac {n^2\hbar^2 \pi^2} {8ma^2}$$not what you have.

 

[vela]

For a symmetric infinite well of width $a$ $$E_n = \frac {n^2\hbar^2 \pi^2} {8ma^2}$$not what you have.

You're confusing the expression with $\hbar$ with the one that uses $h$. It's either
$$E_n = \frac{p_n^2}{2m} =\frac{(\hbar k_n)^2}{2m} = \frac{[\hbar(n \pi/a)]^2}{2m} = \frac{n^2 \hbar^2 \pi^2}{2ma^2}$$ or
$$E_n = \frac{n^2 h^2}{8ma^2}$$ if you use $\hbar \pi = h/2$.

 

[vela]

$P(E_1) = \frac {4}{3}$
$P(E_2) = \frac {1}{3}$

This is clearly wrong. You can't have a probability greater than 1.

You didn't normalize the wave function correctly. If you did, you should have found $P(E_n) = \lvert c_n \rvert^2$.

 

[kuruman]

You're confusing the expression with $\hbar$ with the one that uses $h$. It's either
$$E_n = \frac{p_n^2}{2m} =\frac{(\hbar k_n)^2}{2m} = \frac{[\hbar(n \pi/a)]^2}{2m} = \frac{n^2 \hbar^2 \pi^2}{2ma^2}$$ or
$$E_n = \frac{n^2 h^2}{8ma^2}$$ if you use $\hbar \pi = h/2$.

Actually, the factor of $2^2$ is in confusing a symmetric well $-a\leq x \leq a$ with a symmetric well $-\frac{a}{2}\leq x \leq \frac{a}{2}.$

 

[kuruman]

To @keyzan
The relevant normalized wavefunctions are
$\psi_1(x)=\sqrt{\frac{2}{a}}\cos\left(\frac{\pi x}{a}\right)$
$\psi_2(x)=\sqrt{\frac{2}{a}}\sin\left(\frac{2\pi x}{a}\right)$
Write the given wavefunction as a linear combination of these, not the explicit sinusoidals, as $$\psi(x)=N[A\psi_1(x)+B\psi_2(x)]$$and then simply normalize remembering that the eigenstates $\psi_n(x)$ are orthonormal $$\int_{-\infty}^{+\infty}\psi_k^*(x)\psi_j(x)dx=\delta_{kj}.$$You do not have to perform any integrals.

 

[keyzan]

I understood what I was doing wrong... When I use the formula:
$P(E_1) = \frac{|c_1|^2}{|c_1|^2+|c_2|^2}$

I obviously have to do the complex conjugate of each term. So I get:

$P(E_1) = \frac{\frac {8}{5a}}{\frac {8}{5a} + (\sqrt{\frac {8}{5a}}*\frac{i}{2}+(-\sqrt{\frac {8}{5a}}* \frac{i}{2}))} = \frac{4}{5}$

$P(E_1) = \frac{\frac {2}{5a}}{\frac {8}{5a} + (\sqrt{\frac {8}{5a}}*\frac{i}{2}+(-\sqrt{\frac {8}{5a}}* \frac{i}{2}))} = \frac{1}{5}$

So it all seems fine. Last question... Can I write

$\psi(x) = \sqrt{ \frac {8}{5a}} cos(\frac {\pi x }{a}) + \sqrt{ \frac {8}{5a}} \frac {i}{2} sen(\frac {2 \pi x }{a})$

as:

$\psi(x) = \sqrt{\frac{5a}{10}}*[\sqrt{ \frac {8}{5a}} cos(\frac {\pi x }{a}) + \sqrt{ \frac {8}{5a}} \frac {i}{2} sen(\frac {2 \pi x }{a})]$ ?

That is:

$\sqrt{\frac{1}{|c_1|^2+|c_2|^2}} = \sqrt{\frac{5a}{10}}$

 

[PeroK]

There was a quicker way. We can write:
$$\psi(x)= N\sqrt{\frac a 2}\big (\psi_1(x)+\frac i 2 \psi_2(x)\big )$$Hence:
$$p(E_1) = 4p(E_2)$$And, as these probabilities sum to 1, we have:
$$p(E_1) = \frac 4 5, \ p(E_2) = \frac 1 5$$Also,
$$p(E_1) = N^2\frac a 2= \frac 4 5$$Gives us$$N = \sqrt{\frac 8 {5a}}$$

Note: edited as i got the a/2 upside down.

 

[BvU]

What is $$P(E_1) = \frac{\frac {8}{5a}}{\frac {8}{5a} + (\sqrt{\frac {8}{5a}}*\frac{i}{2}+(-\sqrt{\frac {8}{5a}}* \frac{i}{2}))} = \frac{4}{5}\ ??$$

In part 1 you have established that $N = \sqrt{8\over 5a}$. Post #11 tells you $A = \sqrt{4\over 5}, \ B = \sqrt{1\over 5}$. So $|c_1|^2=4/5$ and $|c_2|^2 = 1/5$.

In the alternative $P(E_1) = \frac{|c_1|^2}{|c_1|^2+|c_2|^2}$ the $c$ don't have to be normalized (that factor drops out) and the 'calculation' is $$P(E_1) = \frac{1^2}{1^2+({i\over 2}) * ({-i\over 2})}$$

$\$

 

[PeroK]

$\psi(x) = \sqrt{\frac{5a}{10}}*[\sqrt{ \frac {8}{5a}} cos(\frac {\pi x }{a}) + \sqrt{ \frac {8}{5a}} \frac {i}{2} sen(\frac {2 \pi x }{a})]$ ?

That doesn't look right. If you express $\psi(x)$ in terms of sines and cosines, the coefficients must have a factor of $\sqrt{ a}$. Whereas, if you express $\psi(x)$ in terms of energy eigenfunctions, then the coefficients will not have such a factor, as this will be included in the eigenfunctions themselves.

Two tips here: 1) always express your wavefunction in terms of the eigenfunctions. With an unknown overall normalisation constant, if necessary. 2) You don't need to calculate the normalisation constant to get the probabilities.

 

[keyzan]

The problem here is that the first point tells me to find N using the normalization condition.

View attachment 340753​

1. Determine the constant N from the normalization condition.

I found N by integrating the square modulus of the function from minus infinity to plus infinity and the result i found is:
$N = \sqrt{\frac{8}{5a}}$
But then the second point tells me:

2. Determine the possible outcomes of an energy measurement and the related probabilities

Now I could insert a new normalization constant so that the sum of the probabilities is 1. But the result I get from this new normalization is:
$N = \sqrt{\frac{5a}{10}}$

which eliminates the $a$ in the $\psi(x)$. Now I wonder, maybe I was wrong to find the N in point 1 and I shouldn't have calculated the integral of the square modulus of the $\psi(x)$ between minus infinity and plus infinity?

Otherwise $a$ is eliminated.

 

[PeroK]

The problem here is that the first point tells me to find N using the normalization condition.




I found N by integrating the square modulus of the function from minus infinity to plus infinity and the result i found is:
$N = \sqrt{\frac{8}{5a}}$

That's correct. I had an error. It's awkward doing this on a phone!

 

[BvU]

In $\psi$ you have a common factor times a cosine plus $i\over 2$ times a sine. The common factor drops out and there are your 4/5 and 1/5 !

$\$

 

[PeroK]

Now I could insert a new normalization constant so that the sum of the probabilities is 1. But the result I get from this new normalization is:
$N = \sqrt{\frac{5a}{10}}$

For the coefficients of the eigenfunctions, the sum of modulus squares is 1). Not for the raw sines and cosines. That's the confusion.

 

[PeroK]

To emphasise the point. The simplest case is where $\psi$ is an eigenfunction:
$$\psi(x) = \psi_1(x) = \sqrt{\frac 2 a}\cos(\frac{\pi x}{a})$$The coefficient when expressed as the eigenfunction is 1. Which equates to probability 1. The coefficient when expressed as a cosine is not 1.