Wavelengths of standing waves on a string

Click For Summary

Homework Help Overview

The problem involves determining the wavelengths of standing waves on a string of fixed length L, which is held at both ends. The task is to find the five longest wavelengths that can fit on the string, expressed in terms of L.

Discussion Character

  • Exploratory, Conceptual clarification, Problem interpretation

Approaches and Questions Raised

  • Participants discuss the relationship between the length of the string and the wavelengths that can fit, with some suggesting drawing the wave patterns to visualize the problem. Questions arise regarding the correctness of reasoning about how wavelengths relate to the string length.

Discussion Status

Participants are actively engaging with the problem, exploring different interpretations of the wavelengths based on visual representations. Some guidance has been provided regarding the relationship between the string length and the wavelengths, though no consensus has been reached on the exact values.

Contextual Notes

There appears to be some uncertainty regarding the application of the formula provided and how it relates to the visual representation of the waves. Participants are also navigating their understanding of the concept of standing waves.

googlyeyes
Messages
17
Reaction score
0

Homework Statement



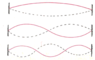
Consider a string of length L held fixed at both ends. The string can be shaken up and down and, at certain frequencies, the result will be a standing wave pattern on the string. Find the five longest wavelengths (call them λ1, λ2, λ3, λ4, and λ5) of the standing wave patterns that fit on the string. Write your answers in terms of L.

Homework Equations



c=fλ

The Attempt at a Solution



λ1 = L
λ2 = L/2
λ3 = L/4
λ4 = L/8
λ5 = L/16
 
Physics news on Phys.org
Have you tried drawing the possible waves?
 
Yes but I am not sure my thinking is right. I am thinking that in order for the wavelength to fit on the string it must either be L (the length of the string) or half, half again, etc. for the entire wave to fit (i am new to physics). Is this thinking completely wrong?
 
The best way to understand is to see it...
 

Attachments

  • Waves.png
    Waves.png
    4.7 KB · Views: 806
So to find the five longest wavelengths do i need to use the formula i gave or should it be obvious (in terms of L) from drawing it?
 
You don't need to use your formula. If the distance between the two black blocks in my image is L. Can you state what the wavelengths of each of the three waves are in terms of L?
 
Ok so the 1st one would be 2L, the 2nd would be L and the 3rd would be 2/3L?
 
googlyeyes said:
Ok so the 1st one would be 2L, the 2nd would be L and the 3rd would be 2/3L?

Correct. What about the 4th and 5th?
 
Um 4th would be 1/2L, 5th would be 2/5L?
 
  • #10
Yup!
 
  • Like
Likes   Reactions: 1 person
  • #11
Thank you so much! I understand this concept so much better now! I really appreciate your help!
 

Similar threads

Determining Steel String Diameter for Standing Wave Node
  • · Replies 1 ·
Replies
1
Views
2K
Length of string in a standing wave
  • · Replies 19 ·
Replies
19
Views
1K
To which natural frequency does wavelength equal to L1
  • · Replies 1 ·
Replies
1
Views
6K
Waves and vibrations on a string
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Reflection of inverted waves to form a standing wave
  • · Replies 3 ·
Replies
3
Views
2K
Actual displacement of a wave particle
  • · Replies 1 ·
Replies
1
Views
2K
Calculating Mass of a Vibrating String Using Known Quantities
  • · Replies 10 ·
Replies
10
Views
2K
Standing Waves On Strings: Harmonic and Frequency Problem
  • · Replies 2 ·
Replies
2
Views
4K
Calculating the length of a string from a standing wave
  • · Replies 4 ·
Replies
4
Views
2K
Standing waves on string with increasing tension
  • · Replies 3 ·
Replies
3
Views
7K