- #1
Albert1
- 1,221
- 0
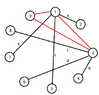
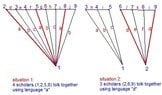
Having 9 scholars attend an international seminar,
the following informations are given:
(1) each member can at most speak 3 different languages
(2) any 3 members at least 2 can communicate
prove:we can find 3 scholars talking together (using one common language)
the following informations are given:
(1) each member can at most speak 3 different languages
(2) any 3 members at least 2 can communicate
prove:we can find 3 scholars talking together (using one common language)