Weight distribution on several floor anchors

[csd]

Hi all,
I am not sure this is the right forum, but I guess my question fits better here than in classical physics.
I am building a lightweight flooring in my utility room to store some "not very heavy" items. Two years back when my house was being finished, I installed two wooden wall plates (175mmx63mm) on each side of the utility room. My plan was to have a flooring that would cover the whole 12 square meters (4 meters long x 3 meters across). So I installed a 4m wall plate on one wall, while on the other one I could only install a 2m wall plate because I had doors and needed to leave space for electrical conduits. So I planned to attach joist hangers to the wall to support the joists.
Back then a friend suggested connecting the wall plate to the wall using chemical anchors, claiming that this would be very strong (supporting up to a ton) even on my wall made of concrete masonry units (not sure about the name in English, but I mean these:

In the end, however, I discovered that each anchor can support around 50kg once you take into account all safety factors. So I decided to make a smaller storage flooring, covering only 2/3 of the room, with something that would look like this, where the two wall plates are in red.

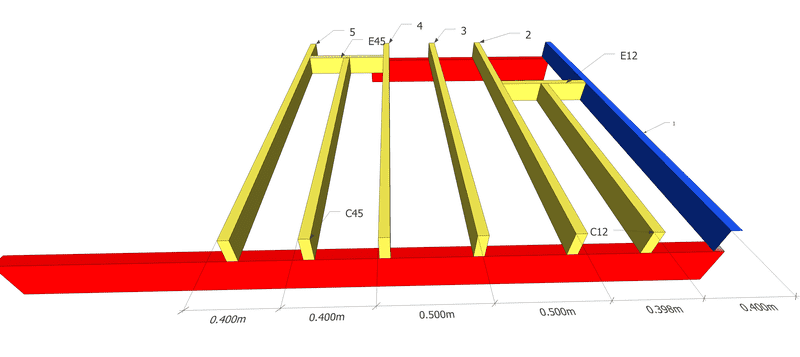
My question is the following. The 4m wall plate is connected to the wall by 8 chemical anchors distributed along its length and spaced by about 50cm. However, the weight supported by the joists will only be distributed along two thirds of the wall plate's length.

My question is the following. How can I compute the load on each anchor knowing the load on each of the joists?
I think this is some sort of beam analysis problem, but I haven't been able to find any free software for MacOS that can help me with this. Can you help me solve this by hand, or using some freely available tool?

Little addition: to make this even more complex, the anchors are not all at the same height. The wall plate looks somewhat like this:

Thanks everyone in advance!

 

[berkeman]

Does this work require a building permit and inspections? Your local building permit department can probably answer these questions better than we can...

 

[csd]

Hi,
no it does not. This is a DIY addition we're making for the purpose of adding some storage space. I thought it would be a relatively common mechanical engineering problem although I do not have the tools to solve it on my own. My computer engineering syllabus excluded construction sciences right before I enrolled ;).

 

[jack action]

How can I compute the load on each anchor knowing the load on each of the joists?

If the wall plate can be assumed to be perfectly rigid, then:

If the joist is right over an anchor, then the entire weight of that joist should be supported by that anchor.

If the joist is in-between 2 anchors, then its weight will be distributed between the 2 anchors.

For example:

      30          40
 _ _ _|_ _ _ _ _ _|_ _
|         |           |
1         2           3

The weight supported by anchors 1, 2 & 3 are:
$$F_1 = 30 \times \frac{2}{5} = 12$$
$$F_2 = 30 \times \frac{3}{5} + 40 \times \frac{2}{6} = 31.3$$
$$F_3 = 40 \times \frac{4}{6} = 26.7$$
You can verify that $F_1+F_2+F_3=30+40$.

IMO, this should be good enough to model your system, at least to get a good first idea about the weight distribution.

 

[csd]

Thanks Jack. This means that if, for example, the leftmost joist is at the midpoint between the first two anchors, the second mid-way between the second and the third, and so on, until the 5, mid-way between the 5th and the 6th, and then there are two more anchors further to the right. We have

half a joist on the first + a portion of the weight of the wall plate
one joist on the second to 5th + a portion of the weight of the wall plate
half a joist on the 6th + a portion of the weight of the wall plate
and ONLY a portion of the weight of the wall plate on the 7th and 8th anchors.

Is this correct?

And what if the wall plate is not perfectly rigid? Actually how do you model non-rigidness? Sometimes I wish my physics courses had gone a little more in depth, although back then I probably would have found it too much too study ;).

 

[csd]

but wait, if we assume it's perfectly rigid, shouldn't the weight be uniformly distributed across all anchors?

 

[jack action]

half a joist on the first + a portion of the weight of the wall plate
one joist on the second to 5th + a portion of the weight of the wall plate
half a joist on the 6th + a portion of the weight of the wall plate
and ONLY a portion of the weight of the wall plate on the 7th and 8th anchors.

Is this correct?

Yes.

And what if the wall plate is not perfectly rigid? Actually how do you model non-rigidness? Sometimes I wish my physics courses had gone a little more in depth, although back then I probably would have found it too much too study ;).

but wait, if we assume it's perfectly rigid, shouldn't the weight be uniformly distributed across all anchors?

In reality, the wall plate should deform under the weight and this should affect the weight distribution. This will depend also on the anchor/wall plate type of joint. Going back to my previous example, looking only at the 30 force, it would push on the anchors 1 & 2 but, due to beam deflection, it could lift the anchor 3. In this case, the weight distribution would slightly be altered. How to do it, would require a very complex model and data that you probably don't even have for this project. The following is a special case of such a problem, still much simpler than yours (source):

 

[csd]

I see, so almost impossible to estimate precisely, right? I guess the safe option is then to ignore the existence of the anchors that are beyond the rightmost joist. What do you think?

Other than that I still have a question.
Back to the idealized case of the perfectly rigid wall plate. If it's perfectly rigid, shouldn't all the anchors contribute in the same manner?

 

[jack action]

It is not a question of ignoring some anchors, it is just that there is no weight on them. Just do the calculations like I did.

For the «perfectly rigid» wall plate, I only meant that it wouldn't deform, therefore pulling and pushing on the anchors. I guessed the better way of explaining the model would be to see it as 7 rigid, independent, wall plates in-between 8 anchors.

 

[csd]

It is not a question of ignoring some anchors, it is just that there is no weight on them. Just do the calculations like I did.

For the «perfectly rigid» wall plate, I only meant that it wouldn't deform, therefore pulling and pushing on the anchors. I guessed the better way of explaining the model would be to see it as 7 rigid, independent, wall plates in-between 8 anchors.

But in practice, the anchors are also not perfectly rigid. So if I put weight on anchors 1 to 6, then these would bend slightly downwards. Wouldn't this bring some weight off them and onto 7 and 8?
Isn't there any nice software I can play with? Besides my garage project, I find this an interesting problem ;).

 

[jack action]

So if I put weight on anchors 1 to 6, then these would bend slightly downwards. Wouldn't this bring some weight off them and onto 7 and 8?

It can be worst than that. It can pull upward onto 7 & 8, meaning it will push harder on the other anchors. If you look at the image I've shown in post #7, using my method, you would have got $W$ on the central support and $\frac{1}{2}W$ on the end supports for a total of $2W$. But the central support reaction is actually slightly larger and the end supports are slightly smaller, but still a total of $2W$.

Like I said, to have a more precise answer, you would require a Finite Element Analysis (FEA) and this would require data input which you could probably not obtain for your project. This mean you would guess those inputs, bringing you back to uncertainties again. IMHO you are better with the simple method I showed you and put a larger safety factor on the result obtained. The problem with nice computer programs is that they give really nice output even with bad inputs, which gives a false sense of confidence.

All you really should care about is will the highest load on one of the anchors be around 20 kgf or 100 kgf. In the first case, you may be OK with 50 kgf anchors, in the 2nd case, you probably won't.

 

[csd]

It can be worst than that. It can pull upward onto 7 & 8, meaning it will push harder on the other anchors. If you look at the image I've shown in post #7, using my method, you would have got $W$ on the central support and $\frac{1}{2}W$ on the end supports for a total of $2W$. But the central support reaction is actually slightly larger and the end supports are slightly smaller, but still a total of $2W$.

Like I said, to have a more precise answer, you would require a Finite Element Analysis (FEA) and this would require data input which you could probably not obtain for your project. This mean you would guess those inputs, bringing you back to uncertainties again. IMHO you are better with the simple method I showed you and put a larger safety factor on the result obtained. The problem with nice computer programs is that they give really nice output even with bad inputs, which gives a false sense of confidence.

All you really should care about is will the highest load on one of the anchors be around 20 kgf or 100 kgf. In the first case, you may be OK with 50 kgf anchors, in the 2nd case, you probably won't.

Thanks, I hadn't thought of this additional load on the other anchors.

Actually, wouldn't it then be better if I cut the wall plate between anchors 6 and 7, thereby removing is additional load?

The thing is that I can live with a maximum load of 40kgf per anchor, but 20kgf is probably too little (the weight of the structure would reach this load by itself).

If I can't count on 40kg per anchor, then I am wondering if I should not add wooden pillars underneath the wall plate. Given the configuration of what's in front, there's no way I can fit in an entire pillar, but I could fit one composed of two pieces. Each anchored to the wall. What do you think?

 

[jack action]

I'm not an expert at this type of construction, I'm not even sure of what you are describing and I don't know what kind of storage will be done in that room, but just by the description you make, my instinct tells me that your installation will not support the weight you expect.

If you count a 40 kgf load on an anchor, I consider that close to 50 kgf. Just imagine a single 75 kg man entering the room and walking on the floor and just happen to stand inline with anchors: that is easily 37.5 kg on each side. Imagine now a dynamic weight, either a man walking (or jumping) or a heavy box that drops on the floor. This kind of dynamic loading scenario can easily double the actual load for a fraction of a second.

If one anchor breaks, then the load on the others increase instantly (dynamically) which means they can break also in some snowball effect.

So if you can reinforce your installation, I think you should. After all, you were expecting a 1-ton anchor that is actually only good for 50 kgf. That tells a lot about what you should do.

 

[csd]

I'm not an expert at this type of construction, I'm not even sure of what you are describing and I don't know what kind of storage will be done in that room, but just by the description you make, my instinct tells me that your installation will not support the weight you expect.

If you count a 40 kgf load on an anchor, I consider that close to 50 kgf. Just imagine a single 75 kg man entering the room and walking on the floor and just happen to stand inline with anchors: that is easily 37.5 kg on each side. Imagine now a dynamic weight, either a man walking (or jumping) or a heavy box that drops on the floor. This kind of dynamic loading scenario can easily double the actual load for a fraction of a second.

If one anchor breaks, then the load on the others increase instantly (dynamically) which means they can break also in some snowball effect.

So if you can reinforce your installation, I think you should. After all, you were expecting a 1-ton anchor that is actually only good for 50 kgf. That tells a lot about what you should do.

Well it's not a room. It's more a big shelf for storing camping stuff and similar things. So the 1-ton anchor was oversized, but 50kgf is definitely very tight, and that's why I am double/triple checking everything. 50kg already takes into account a bunch of safety factors, but I don't want to mess with those.

I was already planning to reinforce the thing by adding hangers to support part of the joist and only have two, or three joists rest on the wall plate. But your reasoning about additional load caused by upward loading of the rightmost anchors makes me doubt this is any good at all. What surprises me is that this idea of a wall plate supported by a large number of anchors seems pretty common practice at least in France.

 

[berkeman]

Thread closed temporarily for Moderation...

 

[berkeman]

Upon further review by the Mentors, this thread will remain closed. Please seek the help of a local Mentor or professional who can help you in-person.