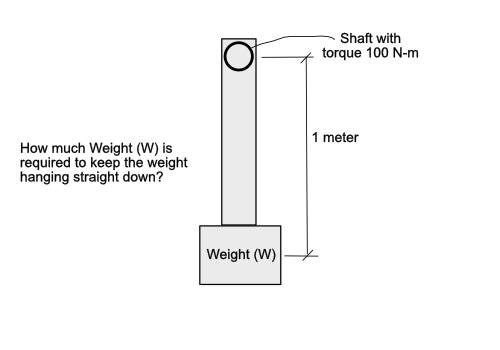
To determine the weight required to keep a weight hanging straight down when torque is known, the discussion explores the relationship between torque and weight on a rotating shaft. It highlights that if the weight is deflected, gravity creates a restoring torque that can be calculated. The conversation also touches on the theoretical implications of infinite weight, suggesting that while finite weight leads to rotation, infinite weight may stabilize the system. Additionally, the discussion raises questions about the perceptibility of macro-scale accelerations over extended periods. Ultimately, the calculations and considerations revolve around balancing torque and weight to maintain stability in the system.