What am I doing wrong with finding the equation of this plane?

[mccoy1]

Hi guys, I did some calculation here and my answer is different from what's given at the end of the book:

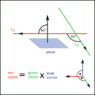
Question: Find an equation of the plane that passes through the point (6,0,-2) and contains the line x= 4-2t, y= 3+5t, z=7+4t.
Book Answer: 33x + 10y + 4z = 190, which is very different from what I got.

How I did it: r =ro + tv.
ro = 4i+3j+7k.
tv =t(-2i+5j+4k).
Po = (4,3,7), P1 = (6,0,-2), so PoP1(vector) = <2, -3, -9>.
The cross product of any two vectors in the plane will give a vector that's perpendicular to the plane (normal n).
So ro X PoP1 = n = <4,3,7>X<22,-3,-9>
Then, the dot product of this normal with any other vector, say <x-6,y,z+2> on the plane gives the equation of the plane. What am I doing wrong. I'd appreciate your input.
Thanks.




H

 

[JeSuisConf]

i think you confused a point in the plane and a vector in the plane. look carefully

 

[mccoy1]

i think you confused a point in the plane and a vector in the plane. look carefully

Thanks for the reply, but I'm lost for sure because I'm no longer thinking now lol.
I took ro as a vector from the origin (i.e from O to point Po) and PoP1 (vector) parallel to vector, V (from origin)...
Can you please point that out. I appreciate your reply.
Cheers

 

[JeSuisConf]

Ok, (6,0,-2) is not a vector parallel to your plane. Here's how you do it:

1. Find any two points on that line
2. The vector between those two points is parallel to your plane
3. The vector between either point in the line and (6,0,-2) is also parallel to your plane

Then you can take the cross product and proceed

 

[PhysDrew]

I think one of the vectors should be between 6i+0j-2k and 4i+3j+7k. Then coss multiply with the other vector.

 

[mccoy1]

Ok, (6,0,-2) is not a vector parallel to your plane. Here's how you do it:

1. Find any two points on that line
2. The vector between those two points is parallel to your plane
3. The vector between either point in the plane and (6,0,-2) is also parallel to your plane

Then you can take the cross product and proceed

Thanks again, I think I haven't said (6,0,-2) is a vector parallel to the plane.

Ok maybe can work on my understanding of the question first? My understanding of the question is that we are not given any vector parallel to the plane, but what we are given is the vector parallel to the line, (vector PoP1) on the plane. This means point Po and point P1 (6,0-2) are the points on the line parallel to vector V. I may be wrong here.

 

[JeSuisConf]

Thanks again, I think I haven't said (6,0,-2) is a vector parallel to the plane.

Ok maybe can work on my understanding of the question first? My understanding of the question is that we are not given any vector parallel to the plane, but what we are given is the vector parallel to the line, (vector PoP1) on the plane. This means point Po and point P1 (6,0-2) are the points on the line parallel to vector V. I may be wrong here.

Ah, right my mistake. However, you did make this type of mistake, because (4,3,7) is not parallel to the plane either.

 

[mccoy1]

I think one of the vectors should be between 6i+0j-2k and 4i+3j+7k. Then coss multiply with the other vector.

Thanks PhysDrew,
Yes, I found that vector to be 2i-3j-9k... and that's where things started to go wrong...

 

[JeSuisConf]

Thanks PhysDrew,
Yes, I found that vector to be 2i-3j-9k... and that's where things started to go wrong...

Yes, exactly. Because you took the cross product: ro X PoP1. But that would require that ro is parallel to the plane. It's not.

 

[PhysDrew]

Yup that's it. It gets the right answer as well (I just checked...phew!)

 

[JeSuisConf]

Basically, you found the vector <2, -3, -9>, and that one is all good. You have everything correct except you want to use <-2, 5, 4> crossed with <2, -3, -9>, and not <4,3,7> crossed with <2, -3, 9>.

 

[PhysDrew]

Thats what I was hinting at in finding the first vector, since you use 4,3,7 in finding that vector, not using it as a vector by itself to get the normal vector.

 

[mccoy1]

Ah, right my mistake. However, you did make this type of mistake, because (4,3,7) is not parallel to the plane either.

No, it's fine.
Again, yes we are not saying (4,3,7) is parallel to the plane. I don't actually have a vector parallel to the plane in the question because any vector parallel to the plane mean that the normal vector of the plane is parallel to that line.

Let explain my reasoning again: I consider point point Po(4,3,7) to be from the origin, thus its vector ro is <4,3,7>. This line Po mets a line PoP1 on the plane, and this line PoP1 is parallel to vector v (from the origin too, just as ro). Vector r, from the origin mets vector PoP1 at point point P1. Now, r = ro + tv, tv = PoP1.
Any comment? thanks guys

 

[mccoy1]

Basically, you found the vector <2, -3, -9>, and that one is all good. You have everything correct except you want to use <-2, 5, 4> crossed with <2, -3, -9>, and not <4,3,7> crossed with <2, -3, 9>.

Yes, exactly. Because you took the cross product: ro X PoP1. But that would require that ro is parallel to the plane. It's not.

Thanks guys, now let me do the calculations. I will let you know the result in a minute.
You both are great :)

Edit: Wow that's it...correct answer. Again, thank you very much (both of you) for helping me understand this.:)

 

[JeSuisConf]

Your explanation is super confusing. I suggest you not think of vectors as "from the origin." Just think of their direction. Think of points vs. vectors.

I think you basically have it all correct but you're overcomplicating your problem.

 

[PhysDrew]

I think the vector from the origin should go to the point (6,0,-2)(the point on the plane), then the first vector will be from 6,0,-2 to 4,3,7. Then cross multiply...

 

[mccoy1]

Your explanation is super confusing. I suggest you not think of vectors as "from the origin." Just think of their direction. Think of points vs. vectors..

Ok sorry about that, but I thought it won't matter and it'll gives us a point of reference as long as the lengths of our vectors are consistent. I thought their tails has to start at certain points (and it doesn't matter which one) and heads end somewhere (which is another point)...I would have also said 'the tails of vector y and z vectors start at point (0,0,0) or at point (blah, blah,blah) and their heads end at blah blah, you know what I mean...just to gives us a point of reference as long as we are consistent (i.e. keeping directions and lengths the same). Well, I may be wrong here again.
Thank you for the help.
Cheers.

 

[mccoy1]

I think the vector from the origin should go to the point (6,0,-2)(the point on the plane), then the first vector will be from 6,0,-2 to 4,3,7. Then cross multiply...

Yes sure: Thanks.
Also, (just as an aside) is there any reason we using the cross products of parallel vectors here (because I think <2, -3,-9> and <-2,5,4> are parallel to each other) to find the vector normal to the plane, instead of using just any other vectors in the plane? I thought a cross product of any two vectors in the plane (doesn't have to be parallel) can give us an equation of a vector orthogonal to the plane.
Cheers.

 

[PhysDrew]

Yes sure: Thanks.
Also, (just as an aside) is there any reason we using the cross products of parallel vectors here (because I think <2, -3,-9> and <-2,5,4> are parallel to each other) to find the vector normal to the plane, instead of using just any other vectors in the plane? I thought a cross product of any two vectors in the plane (doesn't have to be parallel) can give us an equation of a vector orthogonal to the plane.
Cheers.

I don't think they're parallel. I might be wrong here but isn't the magnitude resulting from the cross product of two parallel vecors 0? Thus it would simply represent a point on the plane (ie no magnitude).

 

[mccoy1]

I don't think they're parallel.

Oh sorry, those vectors are not parallel...silly me.
Thanks.

 

[mccoy1]

Hi folks, I'm stuck again on solving a different problem but I don't want to create another thread since it's the same topic:
Question: Find the equation of the line(say L1) that passes through the points (0,1,2) and is parallel to the plane x+y+z =2 and perpendicular to the line(say L2) x = 1+t, y=1-t, z = 2t.
Answer: x = 3t, y=1-t, z = 2-2t.

My attempt:
Direction vector of the plane = <1,1,1>...this is the normal to the plane, call it n. Say <a,b,c> is the directional vector of L1. Since the plane is parallel to the line, the normal the plane is perpendicular to the line, therefor: n.L1 = 0.
So n.L1 = <1,1,1>.<a,b,c> =a+b+c =0...(I)

Direction vector of L2 = <1,-1,2>. Again L1.L2 = 0 since they are perpendicular.
so <a,b,c>.<1,-1,2>=a-b+2c = 0....(II)

Stuck because I need another equation (...(III) ) to be able to find the values of a,b,c but I can't think of where do find it!

Also, If I choose another vector on L1, say <x,y-1,z-2>, then its dot product with both the normal of the plane and direction vector of L2 is also zero...same thing, doesn't seem to help.
Also: I think L2 and normal n are parallel, but looking at their vectors suggests that they are not...why is that? I'm wondering because if n is perpendicular to L1, and we know from the question that L1 and L2 are perpendicular, then n must be parallel to L2.
So can you please help me see where I'm wrong?
Cheers.

 

[HallsofIvy]

Hi folks, I'm stuck again on solving a different problem but I don't want to create another thread since it's the same topic:
Question: Find the equation of the line(say L1) that passes through the points (0,1,2) and is parallel to the plane x+y+z =2 and perpendicular to the line(say L2) x = 1+t, y=1-t, z = 2t.
Answer: x = 3t, y=1-t, z = 2-2t.

My attempt:
Direction vector of the plane = <1,1,1>...this is the normal to the plane, call it n. Say <a,b,c> is the directional vector of L1. Since the plane is parallel to the line, the normal the plane is perpendicular to the line, therefor: n.L1 = 0.
So n.L1 = <1,1,1>.<a,b,c> =a+b+c =0...(I)

Direction vector of L2 = <1,-1,2>. Again L1.L2 = 0 since they are perpendicular.
so <a,b,c>.<1,-1,2>=a-b+2c = 0....(II)

Stuck because I need another equation (...(III) ) to be able to find the values of a,b,c but I can't think of where do find it!

No, you don't need another equation! <a, b, c> is not uniquely defined- any multiple of it is also a direction vector for the same line.

From a+ b+ c= 0, b= -a- c. From a- b+ 2c= 0, b= a+ 2c. Setting those equal, -a- c= a+ 2c so -2a= 3c or c= -(2/3)a. Now b= -a- c= -a+ (2/3)a= -(1/3)a. Any direction vector for the line is of the form <a, -(1/3)a, -(2/3)a>. If you take a= 3, for simplicity, that is <3, -1, -2>.

Also, If I choose another vector on L1, say <x,y-1,z-2>, then its dot product with both the normal of the plane and direction vector of L2 is also zero...same thing, doesn't seem to help.
Also: I think L2 and normal n are parallel, but looking at their vectors suggests that they are not...why is that?

No, they are clearly not parallel. <1 , 1, 1,> is NOT a multiple of <1, -1, 2>!

I'm wondering because if n is perpendicular to L1, and we know from the question that L1 and L2 are perpendicular, then n must be parallel to L2.
So can you please help me see where I'm wrong?
Cheers.

Of course, you could also find a vector that is perpendicular to both <1, 1, 1> and <1, -1, 2> by taking their cross product:
$$(\vec{i}+ \vec{j}+ \vec{k})\times (\vec{i}- \vec{j}+ 2\vec{k}) \left|\begin{array}{ccc}\vec{i} & \vec{j} & \vec{k} \\ 1 & 1 & 1 \\ 1 & -1 & -2\end{array}\right|= 3\vec{i}- \vec{j}- 2\vec{k}$$

 

[mccoy1]

Hi HallsofIvy,
WOW! You are great buddy:). Thank you very much for your help. It's appreciated(by me of course):).
Cheers.

Edit: Ok, yes as I said above and as you have pointed out as well, L1 and n are not parallel...but why? I know that they are not by looking at their numbers in bra & ket , not through understanding.My reasoning is that if L1 and L2 are orthogonal and L1 is orthogonal to n, then n and and vector parallel to L2(which I also called L2 before, but I'll call it v2 this time) must be parallel by default. I know my reasoning is 'faulty' but Can you please help me understand it

 

[HallsofIvy]

Hi HallsofIvy,
WOW! You are great buddy:). Thank you very much for your help. It's appreciated(by me of course):).
Cheers.

Edit: Ok, yes as I said above and as you have pointed out as well, L1 and n are not parallel...but why? I know that they are not by looking at their numbers in bra & ket , not through understanding.My reasoning is that if L1 and L2 are orthogonal and L1 is orthogonal to n, then n and and vector parallel to L2(which I also called L2 before, but I'll call it v2 this time) must be parallel by default. I know my reasoning is 'faulty' but Can you please help me understand it

You are thinking in two dimensions not three. In plane geometry, if two lines are perpendicular to the same line then they are parallel. That is not true in three dimensions. The x-axis and the y-axis are both orthogonal to the z-axis but are not parallel.

 

[mccoy1]

The x-axis and the y-axis are both orthogonal to the z-axis but are not parallel.

Oh thanks, I think i got it now. Two lines may be perpendicular to the same line; but one may be pointing up (up here mean top of the page, direction of z-axis - loosely) while the other one may be pointing into the page..,I think!

 

[Edgardo]

It seems that you have some difficulty visualizing the geometric situation. A good tipp is always to make a sketch of the problem, e.g. when I read your problem I made the sketch in the attachment below.

 

[mccoy1]

when I read your problem I made the sketch in the attachment below.

Thanks for the diagram... I think that' what I meant up there but failed to put it clearly.
Cheers.