- #1
gl0ck
- 85
- 0
Hello,
I got the following diagram, shown below, and I have to derive its transfer function. I think I have a general misunderstanding about the transfer functions. What I think it is, is: output/input basically. As input is the whole block of things that affect the output.
This is the system that I have.
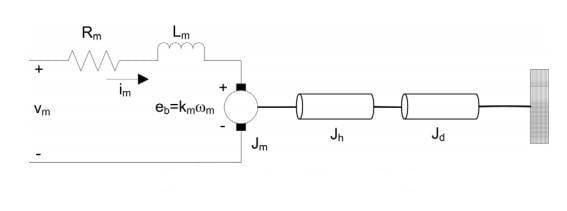
After doing some thinking how to start this I came out with the following:
[tex] v_m ( t ) - R_m i_m ( t ) - L_m { \frac {\ di_m (t) } { dt}} -k_m ω _m ( t ) = 0 [/tex]
It was said that we could ignore the inductance as the motor resistance is much bigger so I came up with as solving for im(t)
[tex] i_m (t) = {\frac {v_m (t) - k_m ω_m (t) }{R_m}} [/tex]
I am given also a expression of the motor shaft equation:
[tex] J_{eq} ω_m (t) = τ_m (t) [/tex] , given that the Jeq is the total moment inertia acting on the motor. Also the torque is given by [tex]τ_m = k_m i_m (t) [/tex]
I also know that the Jeq = Jm + Jh + Jd
With Jm and Jh given in a separate table.
I've found Jd to be [tex] J_d = {\frac {1}{2}} m r^2 [/tex]
So far I've only seen transfer function of an electrical circuit like RC and RL circuits. As I am studying electrical engineering I am kind of confused how I am supposed to derive the transfer function with all this torque and angular velocity. I am asked to derive the transfer function of input voltage and the angular velocity.
I can see that I can substitute what I've found for im into the torque equation, but don't know how then I can turn that into the (s) domain.
Any guidance is much appreciated !
Thanks
I got the following diagram, shown below, and I have to derive its transfer function. I think I have a general misunderstanding about the transfer functions. What I think it is, is: output/input basically. As input is the whole block of things that affect the output.
This is the system that I have.
Homework Equations
After doing some thinking how to start this I came out with the following:
[tex] v_m ( t ) - R_m i_m ( t ) - L_m { \frac {\ di_m (t) } { dt}} -k_m ω _m ( t ) = 0 [/tex]
It was said that we could ignore the inductance as the motor resistance is much bigger so I came up with as solving for im(t)
[tex] i_m (t) = {\frac {v_m (t) - k_m ω_m (t) }{R_m}} [/tex]
I am given also a expression of the motor shaft equation:
[tex] J_{eq} ω_m (t) = τ_m (t) [/tex] , given that the Jeq is the total moment inertia acting on the motor. Also the torque is given by [tex]τ_m = k_m i_m (t) [/tex]
I also know that the Jeq = Jm + Jh + Jd
With Jm and Jh given in a separate table.
I've found Jd to be [tex] J_d = {\frac {1}{2}} m r^2 [/tex]
The Attempt at a Solution
So far I've only seen transfer function of an electrical circuit like RC and RL circuits. As I am studying electrical engineering I am kind of confused how I am supposed to derive the transfer function with all this torque and angular velocity. I am asked to derive the transfer function of input voltage and the angular velocity.
I can see that I can substitute what I've found for im into the torque equation, but don't know how then I can turn that into the (s) domain.
Any guidance is much appreciated !
Thanks
Last edited: