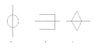What are the different possibilities for the distance function in metric spaces?

[mynameisfunk]

OK, for metric spaces there are apparently 3 different possibilities for the distance function in M where M is the usual Euclidean Plane:

(A) D(u,v) = sqrt((x₁-x₂)² + (y₁-y₂)²)
(B) D(u,v) = max(|x₁-x₂|,|y₁-y₂|)
(C) D(u,v) = |x₁-x₂| + |y₁-y₂|
which somehow correspond to the picture I have attached.
A corresponds to the circle, B to the square and C to the diamond(this is supposed to be a square diamond but i created the image in paint, sorry)
Now, I understand (A) but I cannot seem to understand why (B) and (C) end up looking this way. and to be honest, I don't understand B and C at all.

 

[trambolin]

These are the unit balls with respect to each metric. In other words they mark the points which have the distance "1" to the origin (x_2, y_2) = (0,0). So the first one is a circle equation. The second one has the max of any coordinates, therefore max of (1,1) is 1 which is on the square. So figure out the diamond...

And you have definitely much more choices than 3. These are the most common three.

 

[Landau]

To elaborate on trambolin's last sentence: these three are instances of a special class of metrics defined for every real p>=1:

d_p(x,y)=<br /> \left(|x_1-y_1|^p+|x_2-y_2|^p\right)^{1/p}

(A) corresponds to p=2
(C) corresponds to p=1
(B) is the extension for p=\infty
Besides these p-metrics there are lots of other metrics on R^2.