What Are the Dynamics of a Collar Sliding on a Rotating Rod?

[negatifzeo]

Homework Statement

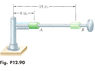
A 3-lb collar can slide on a horizontal rod which is free to rotate about a vertical shaft. The collar is intially held at A by a cord attached to the shaft. A spring constant of 2 lb/ft is attached to the collar and to the shaft and is undeformed when the collar is at A. As the rod rotates at the rate ThetaDot=16 rad/s, the cord is cut and the collar moves out along the rod. Neglecting friction and mass of the rod, determine

a)the radial and transverse components of the acceleration at A

b)The acceleration of the collar relative to the rod at A

c)the transverse component of the velocity of the collar at B

Homework Equations

The Attempt at a Solution

I know the solution to the problem. The answers are
a) Ar=0, Atheta=0

b)1536 in./s^2

c)32.0 in/s

I don't feel like this is a difficult problem, but I am definitely missing a key concept. How can you determine these quantities without r as a function of time?

 

[tiny-tim]

Hi negatifzeo!

(have a theta: θ and an omega: ω and try using the X² tag just above the Reply box )

I don't feel like this is a difficult problem, but I am definitely missing a key concept. How can you determine these quantities without r as a function of time?

I suppose you're wondering how you can find r'' without knowing r(t)?

It doesn't matter, because you can work it out from good ol' Newton's second law … F_radial = m(r'' - ω²r)

 

[negatifzeo]

Hi negatifzeo!

(have a theta: θ and an omega: ω and try using the X² tag just above the Reply box )


I suppose you're wondering how you can find r'' without knowing r(t)?

It doesn't matter, because you can work it out from good ol' Newton's second law … F_radial = m(r'' - ω²r)

The angular velocity is given. The mass is given. But we don't know the total force, do we? The total force is broken up into two components, "e-sub-r" and "e-sub-theta", which we do not know.

 

[tiny-tim]

Hi negatifzeo!

(what hapened to that θ i gave you? )

The angular velocity is given. The mass is given. But we don't know the total force, do we? The total force is broken up into two components, "e-sub-r" and "e-sub-theta", which we do not know.

You won't need the e_θ component of the force.

Try it for a) first. ​