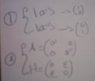What are the eigenvectors |E1> and |E2> of the energy?

[ziad1985]

|a'> and |a"> are both eigenvectors of eigenvalue a' and a" of an Operator A
and a' doesn't equal a",The hameltonien of the system is defined as
H=ε( |a'><a"| + |a"><a'| )
a)What are the eigenvectors |E1> and |E2> of the energy?

b)If the system was in the state |a'> at t=0 , write the system state at t>0

c)What is the probability to find the system in the |a"> state at t>0 if it was in |a'> at t=0?

Frankly the teacher solved it , but i have no idea how he came up with the result in (3) and (4) (For (1)(2)(3)(4) check the pics attached)
I understand (1) and (2) and how we can obtien them,any help for (3) and (4)?

 

[Galileo]

The first thing he did was to write H as a matrix in the basis |a'>, |a''>. You got that part, right?
$$H=\left( \begin{array}{cc}0 & \epsilon \\ \epsilon & 0\end{array}\right)$$

Then (3) you simply find the eigenvectors of this matrix, which is an elementary linear algebra exercise.
Also, if you know the state at a certain time (say t=0) and you've written it out in the basis of energy eigenstates, the time dependence is really simple. Each term simply gets the familiar exponential factor.