- #1
mathdad
- 1,283
- 1
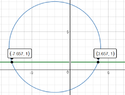
Find values of t such that the points (-2, 3) and (t, 1) are 6 units apart.
The set up is:
6 = sqrt{(t + 1)^2 + {(1 - 3)^2}
I now square both sides to solve for t.
Correct?
The set up is:
6 = sqrt{(t + 1)^2 + {(1 - 3)^2}
I now square both sides to solve for t.
Correct?