What Are the Final Speeds of a Material Point and a Wedge Without Friction?

[Karozo]

Homework Statement

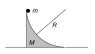
I think that the image is clear.
There isn't friction, not the material point with wedge, not the wedge with the floor.

At time t=0 the material point start to move, I need to find the final speed of the two objects at time $t\rightarrow\infty$.

Homework Equations

I have used conservation of energy and momentum.

The Attempt at a Solution

So I have two equation:
$\frac{1}{2}m{v_m}^2+\frac{1}{2}M{v_M}^2 = mgR$

$m{v_m}+M{v_M}=0$

And the solution is ${v_m}=\sqrt{\frac{mgR}{\frac{1}{2}m+\frac{1}{2}\frac{m^2}{M}}}$

Am I wrong?

 

[tms]

It can be simplified, but it looks okay. What about the velocity of the other object?

 

[Karozo]

Well, if $V_m$ is right is very simple to find $V_M$, so I haven't written it.

 

[Karozo]

I have also a similar problem, you can see the image.

In this the mass m, start with an initial speed $v_0$, you have to find $v_0$ so that the material point has maximum height R.

I think that is right to use the two equations:

$\frac{1}{2}m{v_m}^2+\frac{1}{2}M{v_M}^2+mgR=\frac{1}{2}m{v_0}^2$ energy

$m{v_m}+M{v_M}=mv_0$ momentum

for the point of maximum height, and then you have ${v_m}={v_M}$ , because the two bodies are in contact.

 

[tms]

I have also a similar problem, you can see the image.

Next time, you should put a new problem in a new thread.

In this the mass m, start with an initial speed $v_0$, you have to find $v_0$ so that the material point has maximum height R.

I think that is right to use the two equations:

$\frac{1}{2}m{v_m}^2+\frac{1}{2}M{v_M}^2+mgR=\frac{1}{2}m{v_0}^2$ energy

$m{v_m}+M{v_M}=mv_0$ momentum

for the point of maximum height, and then you have ${v_m}={v_M}$ , because the two bodies are in contact.

That appears correct.