Ackbach
Gold Member
MHB
- 4,148
- 93
I seem unable to get the four necessary equations to solve the following problem:
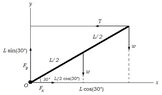
A strut is attached to a wall in such a way that it can pivot. It is currently angled $30^{\circ}$ up from the horizontal, and held in place by a cable. This cable is attached to the wall just above the pivot, and the cable runs out horizontally to the tip of the strut, and then curves over the strut, and down to a weight $w$. The strut is of uniform density, and also has weight $w$. Find the tension in the cable, and the magnitude and direction of the force exerted on the strut by the pivot.
My answer so far: let $\vec{F}_{sp}$ be the force on the strut exerted by the pivot, and let $\vec{F}_{c}$ be the force exerted by the cable on the strut. Let $\theta$ be the angle that $\vec{F}_{sp}$ makes with the horizontal, and let $\varphi$ be the angle that $\vec{F}_{c}$ makes with the negative horizontal. Then the conditions for equilibrium say that
\begin{align*}
F_{sp} \cos( \theta)-F_{c} \cos(\varphi)&=0\\
-F_{c} \sin( \varphi)+F_{sp} \sin( \theta)&=w\\
- \frac{w}{2} \sin(120^{\circ})+F_{c} \sin(150^{\circ}+ \varphi)&=0.
\end{align*}
The first two equations are Newton's Second Law in the $x$ and $y$ directions, respectively, and the third equation is the torque version of Newton's Second Law.
My problem: I cannot find another equation. There are 4 unknowns, and only 3 equations. I tried applying the torque version to another point on the strut (the existing equation was exerted at the pivot), but that does not provide another independent equation.
A strut is attached to a wall in such a way that it can pivot. It is currently angled $30^{\circ}$ up from the horizontal, and held in place by a cable. This cable is attached to the wall just above the pivot, and the cable runs out horizontally to the tip of the strut, and then curves over the strut, and down to a weight $w$. The strut is of uniform density, and also has weight $w$. Find the tension in the cable, and the magnitude and direction of the force exerted on the strut by the pivot.
My answer so far: let $\vec{F}_{sp}$ be the force on the strut exerted by the pivot, and let $\vec{F}_{c}$ be the force exerted by the cable on the strut. Let $\theta$ be the angle that $\vec{F}_{sp}$ makes with the horizontal, and let $\varphi$ be the angle that $\vec{F}_{c}$ makes with the negative horizontal. Then the conditions for equilibrium say that
\begin{align*}
F_{sp} \cos( \theta)-F_{c} \cos(\varphi)&=0\\
-F_{c} \sin( \varphi)+F_{sp} \sin( \theta)&=w\\
- \frac{w}{2} \sin(120^{\circ})+F_{c} \sin(150^{\circ}+ \varphi)&=0.
\end{align*}
The first two equations are Newton's Second Law in the $x$ and $y$ directions, respectively, and the third equation is the torque version of Newton's Second Law.
My problem: I cannot find another equation. There are 4 unknowns, and only 3 equations. I tried applying the torque version to another point on the strut (the existing equation was exerted at the pivot), but that does not provide another independent equation.