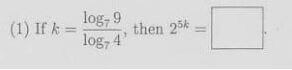What are the possible values of x and y in the equation x + 2y > 5?

  • MHB
  • Thread starter squexy
  • Start date
In summary, the conversation discussed solving an equation and inequality involving variables x and y. The resulting inequalities were x > 0 and y > 2.5. The conversation also touched on the importance of considering positive integers in the solution.
  • #1
squexy
18
0
View attachment 3780

1
x + 2y > 5
x +y> 2,5 (.-1)

x + 2y > 2,5
-x - y > -2,5

y > 2,5
x> 0

View attachment 3779Log 9 - log 4´= log 5

5 * log 5 =
2^5 * 0,6989
2^3,4948
11,27300
 

Attachments

  • qweasdasd.jpg
    qweasdasd.jpg
    2.3 KB · Views: 74
  • qw.jpg
    qw.jpg
    8.6 KB · Views: 74
Mathematics news on Phys.org
  • #2
squexy said:
View attachment 3780

1
x + 2y > 5
x +y> 2,5 (.-1)

x + 2y > 2,5
-x - y > -2,5

y > 2,5
x> 0

How did you get the second inequality? (Thinking)
 
  • #3
evinda said:
How did you get the second inequality? (Thinking)

My apologies, the post was confusing.

n= 5
x + 2y = n
x + 2y > 5
x +y> 2,5
-x - y > -2,5
y > 2,5 - xx+2y > 5
x + 2(2,5 -x) > 5
x>0

x+y>2,5
y > 2,5
 
  • #4
squexy said:
My apologies, the post was confusing.

n= 5
x + 2y = n
x + 2y > 5
x +y> 2,5
-x - y > -2,5
y > 2,5 - xx+2y > 5
x + 2(2,5 -x) > 5
x>0

x+y>2,5
y > 2,5
How did you get to the inequality $x+y>2.5$ ?
 
  • #5
evinda said:
How did you get to the inequality $x+y>2.5$ ?

I divided 5 by 2.
x + 2y > 5
x + y > 5/2
x + y > 2,5
 
  • #6
squexy said:
I divided 5 by 2.
x + 2y > 5
x + y > 5/2
x + y > 2,5

If you want to divide by 2, the inequality will become $\frac{x+2y}{2} > \frac{5}{2} \Rightarrow \frac{x}{2}+y>2.5$.
 
  • #7
evinda said:
If you want to divide by 2, the inequality will become $\frac{x+2y}{2} > \frac{5}{2} \Rightarrow \frac{x}{2}+y>2.5$.

So I should not divide by 2 otherwise I will get x=0, I must be wrong from the begging how could I start to solve the 1 question?
 
  • #8
squexy said:
So I should not divide by 2 otherwise I will get x=0, I must be wrong from the begging how could I start to solve the 1 question?

We add $x$ to $2y$ in order to get $n$. So notice that both of them have to be $\leq n$. You also have to take into consideration the fact that we are looking for positive integers.
 

FAQ: What are the possible values of x and y in the equation x + 2y > 5?

What is the equation for satisfaction?

The equation for satisfaction is a complex and subjective concept that varies from person to person. It is often described as a balance between expectations and reality, where satisfaction is achieved when expectations are met or exceeded.

How can I satisfy the equation in my personal life?

Satisfying the equation in your personal life involves understanding your own expectations and needs, setting realistic goals, and actively working towards achieving them. It also involves finding a balance between your personal desires and the expectations of others.

Is there a formula for satisfying the equation in a professional setting?

There is no one-size-fits-all formula for satisfying the equation in a professional setting. However, some common factors that contribute to job satisfaction include feeling valued and recognized, having a good work-life balance, and having opportunities for growth and development.

Can satisfying the equation lead to long-term happiness?

Satisfying the equation can certainly contribute to long-term happiness, as it involves finding a balance and meeting expectations in various aspects of life. However, happiness is a complex and multi-faceted concept that cannot be reduced to a single equation.

What role does external factors play in satisfying the equation?

External factors, such as societal expectations, cultural norms, and economic conditions, can certainly influence our ability to satisfy the equation. However, it is important to remember that we have control over our own expectations and reactions, and can work towards finding satisfaction despite external factors.

Similar threads

MHB [ASK] A Line Intercepting A Circle
Replies
4
Views
1K
MHB -s6.6 solve exponential eq 3^x-14\cdot 3^{-x}=5
Replies
1
Views
859
I A doubt about the multiplicity of polynomials in two variables
Replies
8
Views
2K
B Wolfram Alpha's Why the 2 i π n?
Replies
3
Views
1K
MHB [ASK] Make x and y the Subjects: x^3-3xy^2=a, 3x^2y-y^3=b
Replies
6
Views
2K
B Natural Numbers contain all the Primes
Replies
24
Views
2K
A The Last Occurrence of any Greatest Prime Factor
Replies
7
Views
1K
MHB Solving Trig Identity: Sin[1/2 sin^−1 (x)] = 1/2 X (sqr(1+x) –sqr(1-x))
Replies
2
Views
1K
MHB What is the Value of \(x^5+y^5+z^5\) Given Initial Polynomial Conditions?
Replies
1
Views
2K
MHB Solve Inequality & Simul Eqns: Alg Workings Q (a,b,c)
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top