What Are the Relativistic Implications for Beacon Synchronization?

[dom_quixote]

I propose to you a kinematics problem described by classical physics.

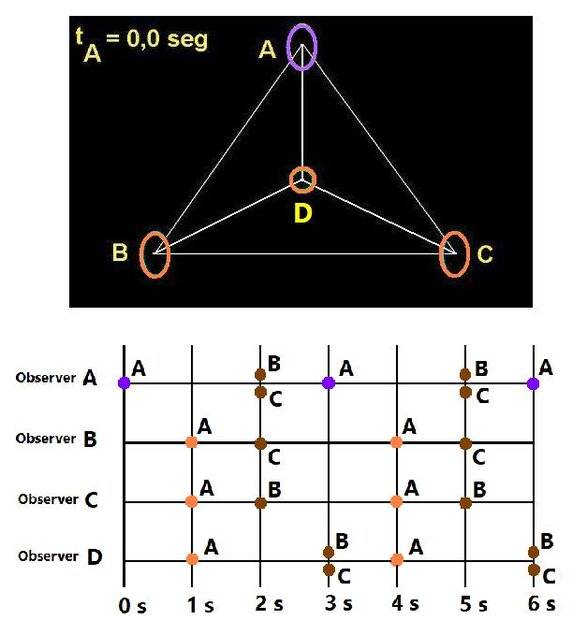
Three space beacons A, B and C are 300,000,000 m (approximately one light second) apart.

Beacon A emits a bright flash every three seconds. Beacons B and C respond instantly to the flash of Beacon A by emitting "synchronized" flashes.

In Beacons A, B and C there is an observer in each of them. There is also an observer at an Passive Watch Post D, which is equally 300,000,000 m away from Beacons A, B and C.

Below the figure of the observation system there is a time chart in which the flashes apparently observed in Beacons A, B and an Passive Watch Post C are graphically recorded.

It is known through the Theory of Relativity that there is no absolute simultaneity, this depends on the frame of reference.

I would like to know what the implications are when the problem is analyzed by relativistic physics.

 

[Ibix]

What do you mean, what are the implications? The beacons flash according to the rules you've set up. Different frames won't get the same timings you've shown, which appear to be shown in the mutual rest frame of the four observers, but that doesn't really change anything.

Since you've got the x, y, z, and t coordinates of all relevant events already listed, just plug them into the Lorentz transforms to get the coordinates in any other frame.

 

[Dale]

Your Observer D seems wrong.

 

[DaveC426913]

The diagram taken without context is ambiguous, and that kind of threw me.

It could represent a 2D arrangement, with A, B and C arranged radially round D.
It could represent a 3D arrangement, with A, B and C along orthogonal paths from D.

But the text belies these possibilities:

"...A, B and C are 300,000,000 m (approximately one light second) apart..."
"...Watch Post D, which is equally 300,000,000 m away from Beacons A, B and C..."

It's a tetrahedron, with A, B C and D all being equidistant from each other.

Also, it's not entirely clear what your colours represent. At first, I thought they were a purple, orange and brown light for clarity, but no.

 

[Orodruin]

As Dale says, D is wrong. If all beacons are equidistant, then the flash from any beacon must reach all other beacons at the same time.

 

[DaveC426913]

 

[Vanadium 50]

I would like to know what the implications are when the problem is analyzed by relativistic physics.

What does this mean?

 

[dom_quixote]

As Dale says, D is wrong. If all beacons are equidistant, then the flash from any beacon must reach all other beacons at the same time.

Thanks, Orodruin!

You are right and I am wrong. I should have said that beacons B and C are only sensitive to the light pulse from beacon A.

 

[dom_quixote]

What do you mean, what are the implications? The beacons flash according to the rules you've set up. Different frames won't get the same timings you've shown, which appear to be shown in the mutual rest frame of the four observers, but that doesn't really change anything.

Since you've got the x, y, z, and t coordinates of all relevant events already listed, just plug them into the Lorentz transforms to get the coordinates in any other frame.

Thanks, Ibix!
I think I found a particular situation in which it is possible to determine the simultaneity of two events, that is: beacons B and C flashing at the same time.

 

[PeterDonis]

the simultaneity of two events

Will depend on which frame you choose. As you've defined the problem, it looks like all of the beacons are at rest relative to each other, and B and C are both separated from A by the same distance in the frame in which all of the beacons are at rest, so in that frame B and C will both flash at the same time.

 

[Janus]

Thanks, Ibix!
I think I found a particular situation in which it is possible to determine the simultaneity of two events, that is: beacons B and C flashing at the same time.

I think you might be confused as what "frame of reference" means in Relativity. In SR it generally means an inertial frame of reference. And it isn't the same as "point of view". The defining characteristic for differentiating different frames of reference are their relative motion with respect to each other, not physical separation. Since all your beacons are at rest with respect to each other, they are "in" the same reference frame.
The fact that all the beacons can agree on simultaneity events is not contrary to Relativity.
What Relativity says is that inertial frames in motion with respect to each other will not agree on simultaneity. Thus if you duplicated this setup and had the second setup in motion with respect to the first, then you'd have situation where the two setups would not agree on simultaneity. Each set up would say its beacons flashed simultaneously, while the beacons in the other setup did not.

 

[Vanadium 50]

it is possible to determine the simultaneity of two events, that is: beacons B and C flashing at the same time.

Then there is no need for D. If you find that you need to add extraneous elements, its a sign you are misthinking things.

Further, if your whole system is moving, B and C may no longer be simultaneous.

 

[Ibix]

I think I found a particular situation in which it is possible to determine the simultaneity of two events, that is: beacons B and C flashing at the same time.

Of course it's possible to determine that, given a definition of a simultaneity convention. Your apparatus relies on Einstein's synchronisation convention, (in fact, it's just a needlessly complicated version of the Einstein's Train thought experiment) and other frames will not agree that B and C flashed simultaneously. You can calculate how the motion of the beacons cancels out with the lack of synchronisation so that pulses arrive simultaneously at D without leaving B and C simultaneously by using the Lorentz transforms, as I suggested in #2.

 

[DaveC426913]

Further, if your whole system is moving, B and C may no longer be simultaneous.

Wait, what? Moving relative to what?

Technically, the whole system is moving right now (relative to, say, Barnards Star). And they still appear simultaneous.

 

[Ibix]

Moving relative to what?

Whatever reference frame you use to analyse it.

It's just Einstein's train with bells on. B and C only flash simultaneously in one frame, the one where the apparatus is at rest, just like the lightning bolts in the normal version.

 

[DaveC426913]

Whatever reference frame you use to analyse it.

OK. That was a bit ambiguous and needed clarifying.

 

[Orodruin]

It's just Einstein's train with bells on. B and C only flash simultaneously in one frame

Considering this is a 3D setup, they flash simultaneously in any frame where their separation is orthogonal to the frame’s velocity relative to the rest frame.

 

[Ibix]

Considering this is a 3D setup, they flash simultaneously in any frame where their separation is orthogonal to the frame’s velocity relative to the rest frame.

I was actually meaning to come back and correct myself on that point but I didn't get round to it - thanks.

 

[Dale]

I think I found a particular situation in which it is possible to determine the simultaneity of two events, that is: beacons B and C flashing at the same time.

You did determine that they are simultaneous in their rest frame. You did not determine that they are simultaneous in any other frame.

 

[dom_quixote]

Thank you all. Regarding the adoption of a specific frame of reference, what would happen to the proposed system if I adopted the entire universe as a frame of reference?

 

[Ibix]

Thank you all. Regarding the adoption of a specific frame of reference, what would happen to the proposed system if I adopted the entire universe as a frame of reference?

The question makes no sense. The universe is not a frame of reference.

 

[DaveC426913]

Thank you all. Regarding the adoption of a specific frame of reference, what would happen to the proposed system if I adopted the entire universe as a frame of reference?

You're going to have to place a (stationary) observer somewhere in your FoR; they can't be everywhere. And they can't be simultaneously moving at different velocities (although you can have as many observers - each moving at their own peculair velocity - as you want).

 

[Nugatory]

Thank you all. Regarding the adoption of a specific frame of reference, what would happen to the proposed system if I adopted the entire universe as a frame of reference?

A frame of reference is a convention for assigning coordinates (position x,y,z at time t) to events (for example beacon A was here when it flashed). It’s not clear what “adopting the entire universe as a frame of reference” would mean.

 

[dom_quixote]

You're going to have to place a (stationary) observer somewhere in your FoR; they can't be everywhere. And they can't be simultaneously moving at different velocities (although you can have as many observers - each moving at their own peculair velocity - as you want).

Thanks, Dave!
To see the entire universe as a single frame of reference, the observer would need to have superpowers, for example being everywhere at once.

 

[jbriggs444]

To see the entire universe as a single frame of reference, the observer would need to have superpowers, for example being everywhere at once.

This hypothetical superpower (faster than light measurement) is problematic. It either violates the postulates on which special relativity is based or it allows for causality violation. For this reason, that particular superpower is not considered physically reasonable.

https://en.wikipedia.org/wiki/Tachyonic_antitelephone

 

[PeterDonis]

To see the entire universe as a single frame of reference, the observer would need to have superpowers, for example being everywhere at once.

This is getting into personal speculation, which is off limits here. Since the OP has been sufficiently discussed, this thread is now closed. Thanks to all who participated.