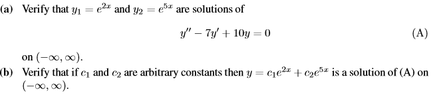- #1
ineedhelpnow
- 651
- 0
(Wave)
i have a test on friday that I am studying for so i was working through some problems in my textbook. i came across this question and I am stuck on what to do. can anyone help me out?
thanks
View attachment 4128
i have a test on friday that I am studying for so i was working through some problems in my textbook. i came across this question and I am stuck on what to do. can anyone help me out?
thanks
View attachment 4128