MHB What Are the Values of a and b for a Cubic Curve's Tangent Line?

[MarkFL]

Here is the question:

Curve Tangent Question?

Hello,

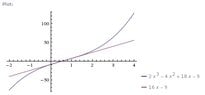
The line y = 16x - 9 is a tangent to the curve y = 2x^3 + ax^2 + bx - 9 at the point (1, 7).
Find the values of a and b.

Thanks in advance.
-Covert

Here is a link to the question:

Curve Tangent Question? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Re: Covert's question at Yahoo! Answers regarding a line tangent to a cubic and fnding parameters

Hello Covert,

Let's define:

$f(x)=2x^3+ax^2+bx-9$

We are given that the point (1,7) is on the curve, so we must have:

$f(1)=2(1)^3+a(1)^2+b(1)-9=2+a+b-9=a+b-7=7\,\therefore\,a+b=14$

We also know that at the point (1,7), $f(x)$ must have a gradient of 16, the same as the line. Hence, we may compute the derivative of $f(x)$, and then set $f'(1)=16$:

$f'(x)=6x^2+2ax+b$

$f'(1)=6(1)^2+2a(1)+b=6+2a+b=16\,\therefore\,2a+b=10$

We now have the linear system:

$a+b=14$

$2a+b=10$

Subtracting the first from the second, we eliminate $b$ to obtain:

$a=-4$

Substituting for $a$ into the first equation, we find:

$b=18$

Here is a graph showing the function and its tangent line at the given point:

View attachment 584