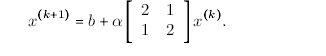natalia
- 6
- 0
Considering the following
View attachment 2409
find the values for α for any initial value of x(0).
Any help will be useful, thank you!
View attachment 2409
find the values for α for any initial value of x(0).
Any help will be useful, thank you!