What Defines the Regions of Absolute Stability in Numerical Methods?

[evinda]

Hello! (Wave)

We have to look for numerical methods for the numerical solution of $\left\{\begin{matrix}
y'(t)=f(t,y(t)) &, a \leq t \leq b \\
y(a)=y_0 &
\end{matrix}\right.$ that have 'great' regions of absolute stability.

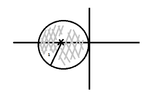
Methods of which the region of absolute stability contains the whole left complex semiplane are calles $A-$ stable.

View attachment 4113

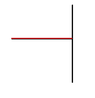
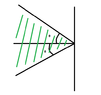
Since at applications we often see systems with matrices with real ( negative ) eigenvalues, or eigenvalues at a region $S_{\theta}, \theta \in \left( 0, \frac{\pi}{2} \right), S_{\theta}:=\{ z \in \mathbb{C} z=\rho e^{i \phi}, \pi-\theta<\phi< \pi+\theta, \rho>0 \} $, it isn't necessary to resort to a $A-$ stable method , but it suffices to work with a method, of which the region of absolute stability contains the negative real semiaxis or the region $S_{\theta}$, respectively. Such methods are called $A_0-$ stable and $A(\theta)-$stable, respectively.

View attachment 4114

View attachment 4115
Could you explain me why the graph for the $A(\theta)-$stable method looks like that?

Furthermore, what is the main difference between $A, A_0$ and $A(\theta)$- stable methods?

Also, for the $A_0-$stable method, is the region of absolute stability this one: $\{ z \in \mathbb{C}: z=\rho e^{i \phi}, \pi<\phi< \pi, \rho>0 \}$? If so, could you explain me why it is like that?

 

[jvicens]

Hello!

The graph for an $A(\theta)-$stable method looks like that because it represents the region of absolute stability for the method. The region of absolute stability is a region in the complex plane that indicates the values of the step size and the eigenvalues of the system that guarantee convergence of the numerical method. In other words, the method will give accurate results for any values within this region.

The main difference between $A, A_0,$ and $A(\theta)-$stable methods lies in the shape of their respective regions of absolute stability. As mentioned in the forum post, $A-$stable methods have a region that contains the entire left complex semiplane, while $A_0-$stable and $A(\theta)-$stable methods have regions that contain the negative real semiaxis and the region $S_{\theta}$, respectively. This means that $A-$stable methods are more robust and can handle a wider range of eigenvalues, while $A_0-$stable and $A(\theta)-$stable methods are more specialized for specific types of systems.

For the $A_0-$stable method, the region of absolute stability is indeed $\{ z \in \mathbb{C}: z=\rho e^{i \phi}, \pi<\phi< \pi, \rho>0 \}$. This is because the method is designed to handle systems with negative real eigenvalues, which are represented by the negative real semiaxis in the complex plane. The region of absolute stability for this method ensures that the numerical solution will converge for any step size and eigenvalues within this region.