What determines the time constant in a parallel R and C circuit?

[PhysicsTest]

TL;DR Summary

Understanding the R and C parallel circuit

If i have the R and C circuit in parallel,

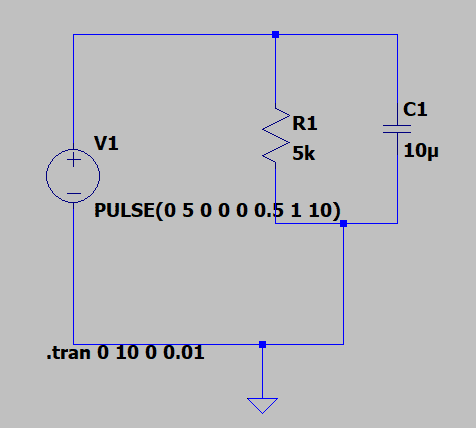
the battery voltage is completely applied to the capacitor of 10uF since it is in parallel, but as per the capacitor behavior it shall charge slowly. So which is correct? I mean is it wrong connection?

 

[TonyStewart]

Yes, there is a false assumption in understanding.

Imagine (from now on) that every battery, or voltage supply AND every capacitor has some finite resistance in series. It might be milliohms but it never zero, yet for logic diagrams it is almost never shown. ( see TI's Webench designs for voltage regulators for exceptions so that inrush currents can be estimated.)

What limits the capacitor charge current? V/ESR ?

It is not shown except in your new real perspective (from now on), except the effective series resistance (ESR) is real but unknown or unspecified in your image.

What limits the discharge current only if V1 is disconnected? Is it the ESR or R1 with C?

In that case, the negligible unstated ESR or series resistance is ignored since R1 is significantly larger.

Look up the formula for approximating capacitor current from its current limiting series resistor and voltage change rate dV/dt.

 

[berkeman]

I mean is it wrong connection?

Yes it is incorrect, as Tony has pointed out. Also, I'm surprised that SPICE did not throw an error for that connection of an ideal voltage source to a capacitor. Does the model for the V1 source include an output resistance that you've set to a non-zero value?

 

[Baluncore]

The circuit is suspicious as an LTspice simulation for several reasons.

1. You have connected a capacitor across a (pulse) voltage source, without a specified series resistance, Rs. You would expect high currents during voltage transitions.

2. The pulse rise and fall times are specified as zero, which luckily will default to some sane proportion of the on time, or you would see an infinite current from the voltage source.

3. You have an 0.5 sec pulse duration, with a maximum simulation time step of 0.1 sec, (with pulse transition times of zero). Let LTspice default Tmaxstep.

 

[DaveE]

As others have pointed out, the the real world, there will always be some series resistance.

But I think it's also important to understand the world of networks with idealized components. Every schematic is wrong, schematics are a simplification of the incredibly complex world of electricity and magnetism. There is an art to modeling, or communication with other EEs, with schematics; i.e. what you choose to show and what you choose to leave out. Sometimes a wire with 2mΩ of resistance can be ignored, other times it's really important.

When you start modeling circuits with ideal components there are somethings that don't make sense. When you do the math there is no answer, or you get infinite results. Here are a couple of things to look out for:

1) Any loop in a network that contains only voltage sources and capacitors. Except for the trivial case where the initial conditions match perfectly and the voltage source waveforms are smooth*. This will result in infinite currents in the solution. This is a sign that you need to include some series resistance in that loop to remove the infinities.

2) The dual case: Any node in a network that connects only current sources and inductors. Except for the trivial case where the initial conditions match perfectly and the current source waveforms are smooth*. This will result in infinite voltages in the solution. This is a sign that you need to include some shunt resistance at that node to remove the infinities.

This is why @berkeman was surprised that LTSpice would let you do this. Your circuit is an idealized model that doesn't make sense. It's why experienced EEs immediately respond with comments about the model accuracy and not about the results.

*By smooth I mean the 1^st derivative (the slope) is always finite.

 

[PhysicsTest]

Ok i understand that the circuit is wrong.

I am going wrong every time i analyze a circuit, I have slightly modified the circuit
Here i have applied DC 5V.
Step1: When 5V applied the capacitor is initially discharged that is 0V, hence it is short circuit the current flowing will be
i = 5 / 10k = 0.5mA.

Step2: The capacitor slowly charges with time constant of R1*C1 = 5k*10uF = 0.05 seconds
V = 5(1 - e^(-t/0.05))

Step3: When the capacitor is fully charged, the capacitor is open circuit hence the current is
i = 5 /(5 + 10)k = 5/15k = 0.33mA.
Is my analysis correct?

 

[berkeman]

Step2: The capacitor slowly charges with time constant of R1*C1 = 5k*10uF = 0.05 seconds
V = 5(1 - e^(-t/0.05))

I don't think that is correct. There are two resistors in the circuit, which affects the charging/discharging behavior and time constant.

Can you write the KCL equations for this circuit and solve them to find out the actual time constant?

 

[Baluncore]

For an LTspice simulation, the 5 volt DC supply will cause the capacitor to have an initial operating point before the simulation starts of;
Vc = 5 volts * 10k / ( 5k + 10k ) = 3.333 V.

Now you have the series resistor, R2 = 10k, you can use a voltage pulse to simulate the capacitor starting at zero and charging exponentially towards 3.333 volts.

 

[DaveE]

Can you write the KCL equations for this circuit and solve them to find out the actual time constant?

Yes, this! You'll learn a lot more about electronics if you solve simple circuits with math before you simulate them. Simulations only give you answers, not reasons.

 

[LvW]

Step2: The capacitor slowly charges with time constant of R1*C1 = 5k*10uF = 0.05 seconds
V = 5(1 - e^(-t/0.05))Is my analysis correct?

No - the used time constant is NOT correct.
Simple trick: Ask yourself about which resistor combinaton the C will be discharged, when the voltage source is replaced by a short circuit.

 

[TonyStewart]

If you understand Thevenin equivalent circuits, then you will immediately understand the correct solution to the current limit and voltage limit with the V1 and the Resistor network reduced to a single Rth value and a Vth value.

 

[PhysicsTest]

I don't think that is correct. There are two resistors in the circuit, which affects the charging/discharging behavior and time constant.

Can you write the KCL equations for this circuit and solve them to find out the actual time con

I am struck up at solving the below integral equation for current i2.

The equation is getting complicated.

 

[TonyStewart]

your KCL is the hard way.

The Thevenin approach as I suggested is trivial to combine V1 R1,R2 into Vth, Rth Thevenin values

https://www.allaboutcircuits.com/textbook/direct-current/chpt-10/thevenins-theorem/#:~:text=Thevenin's theorem states that all,it with an open circuit.

There are other methods for more complex circuits.

 

[DaveE]

your KCL is the hard way.

The Thevenin approach as I suggested is trivial to combine V1 R1,R2 into Vth, Rth Thevenin values

https://www.allaboutcircuits.com/textbook/direct-current/chpt-10/thevenins-theorem/#:~:text=Thevenin's theorem states that all,it with an open circuit.

There are other methods for more complex circuits.

Yes, that's the easy way, but he may not know that method yet.
Plus, there is some value in doing a simple circuit like this using basic methods.

 

[DaveE]

View attachment 329931

I am struck up at solving the below integral equation for current i2.
View attachment 329932
View attachment 329933
The equation is getting complicated.

First of all, great work doing KVL equations, those look good. Except when you take the derivative of both sides, $V1$ doesn't go away, unless it's really a constant value (always, from the big bang until the heat death of the universe). So that should be $\frac{dV1}{dt}$.

However, the time constant of the circuit doesn't depend on the driving function, so you're either really smart and didn't tell us, or you were lucky. Anyway, your equation isn't complicated, it's essentially done.

So, you know $i_2 = e^{-kt}$ what is the time constant for $i_2$ then?

BTW, most EEs would write $\frac{(1+\frac{R2}{R1})}{R2} = \frac{R1+R2}{R1R2} = \frac{1}{R1||R2}$. Sometimes things that look complicated just haven't been expressed in a simple way. With practice you will learn more shortcuts and standard equation formats so that things are easier to do and/or understand.

 

[PhysicsTest]

I was worried of the calculation of the voltage across the capacitor,

The time constant is k = (R1 + R2)/(R1R2C)
Yes i will try to solve using Thevenin, thank you all for support, i could solve one equation.

 

[LvW]

The time constant T has the unit "s" (V/A)*(As/V)=Ohm*Farad

 

[DaveE]

In $e^{-\frac{t}{\tau}}$, the time constant is $\tau$. The argument for the exp function must be dimensionless.

 

[hutchphd]

Ohm-Farad is time so what is the issue?

 

[PhysicsTest]

The time constant is 1/k = R1R2C/(R1+R2) = (R1||R2)*C seconds.

 

[DaveE]

The time constant is 1/k = R1R2C/(R1+R2) = (R1||R2)*C seconds.

Yes, good work!

 

[DaveE]

the time constant of the circuit doesn't depend on the driving function

Let me expand on this statement a bit. It's important to understand. All of this applies to linear networks (circuits).

The time constant(s) (yes, there could be more than one; actually IRL, there often is.) are a feature of the circuit, independent of its inputs. In the same way that a white car is white in London or Atlanta; going 20mph or 75mph. This means that all of the INDEPENDENT sources can be set to zero. Then you can develop the dynamic equations (KVL, KCL...) that will describe how the circuit responds. I think the best way to think of this is the circuit's response to it's non-equilibrium initial conditions. So, for your circuit, the best way to think of this is to short the voltage source (if there were a current source you would replace it with an open branch) and then put some initial charge (or voltage) on the capacitor. The problem you are left to solve is how quickly the capacitor discharges.

When you have your circuit equations (KVL, etc.) you will be left with some differential equations. The circuits' time constant(s) are the constants in each exponential term in the homogeneous solution. Yes, they are all exponentials, that's why I stipulated that it has to be a linear circuit.