- #1
APUGYael
- 41
- 1
Hey all,
Here's a neat picture:
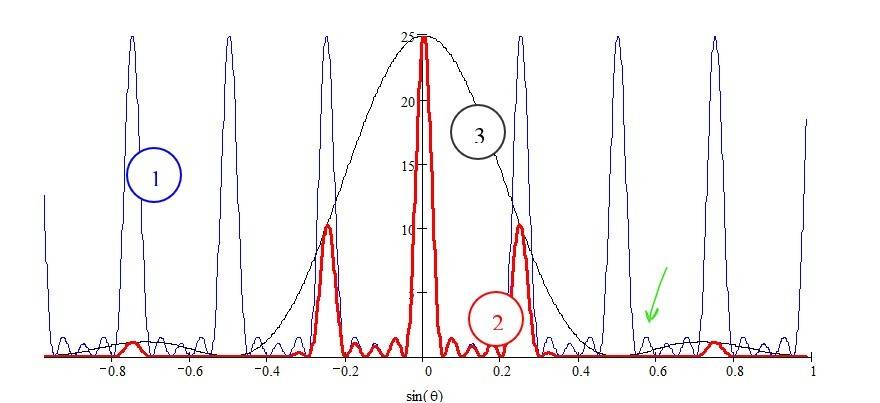
The green arrow points towards one of the submaxima that I am curious about. It's the submaximum of the curve labeled 1.
1. represents the interference pattern
3. represents the diffraction pattern
2. represents the irradiance pattern
I guess that those maxima are created by waves not being 100% constructive or destructive (but rather somewhere in between, e.g. slightly destructive). Is that the right explanation?
While I am on this subject, what is the difference between all the different curves. Is curve 2 the result of combining curve 1 and 3?
EDIT: Picture not working?
Here's a direct link. Remove the space next to the . of .com
https://imgur. com/a/qMfzW8E#btBKyBH
EDIT: Solved.
https://phys.libretexts.org/Bookshe..._Interference/3.3:_Multiple-Slit_Interference
Here's a neat picture:
The green arrow points towards one of the submaxima that I am curious about. It's the submaximum of the curve labeled 1.
1. represents the interference pattern
3. represents the diffraction pattern
2. represents the irradiance pattern
I guess that those maxima are created by waves not being 100% constructive or destructive (but rather somewhere in between, e.g. slightly destructive). Is that the right explanation?
While I am on this subject, what is the difference between all the different curves. Is curve 2 the result of combining curve 1 and 3?
EDIT: Picture not working?
Here's a direct link. Remove the space next to the . of .com
https://imgur. com/a/qMfzW8E#btBKyBH
EDIT: Solved.
https://phys.libretexts.org/Bookshe..._Interference/3.3:_Multiple-Slit_Interference
Last edited:

 Thereby logic dictates I haven't ... see the edit in #18
Thereby logic dictates I haven't ... see the edit in #18