What Does About x = 3 Mean in Volume Calculation?

[shamieh]

Find the Volume of a Solid by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer.

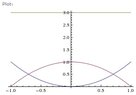
\(\displaystyle x = y^2\), \(\displaystyle x = 1 - y^2\), about \(\displaystyle x = 3\)

So here is how far I've gotten with this problem. I need help though. Any guidance will be greatly appreciated.. One of the problems is I don't understand what "about x = 3" means exactly? Like what do they mean "about x = 3?" Anyways here is what I have:

I have a right and left parabola basically. I set the two equal to each other to find lines of intersection.

\(\displaystyle
y^2 = 1 - y^2\)

thus;
\(\displaystyle y = \frac{\sqrt{2}}{{2}}\)So I know the areas are even symmetry so I can say \(\displaystyle 2\pi \int^\frac{\sqrt{2}}{2}_0 (Right - left)dy \)

right?

so am i correct in saying \(\displaystyle 2\pi \int^\frac{\sqrt{2}}{2}_0 (1 - y^2)^2 - (y^2)^2 dy\)?

 

[MarkFL]

Here is a plot:

View attachment 1859

Imagine the plot rotated 90° clockwise. Now the outer radius of an arbitrary washer will be the distance between the axis of rotation $x=3$ and the function $x=y^2$, while the inner radius will be the distance from the axis of rotation and the function $x=1-y^2$.

You are correct that you can use symmetry as follows:

\(\displaystyle V=2\pi\int_0^{\frac{1}{\sqrt{2}}} (\text{outer radius})^2-(\text{inner radius})^2\,dy\)

Can you find the radii?

 

[shamieh]

\(\displaystyle 2\pi \int ^\sqrt{2/2}_0 (3 - y^2)^2 - (3 - (1 - y^2)^2 dy \)

\(\displaystyle 2\pi \int^\sqrt{2/2}_0 9 - 6y^2 + y^4 - 3 + 1 + 2y^2 - y^4\)

\(\displaystyle = 2\pi \int^\sqrt{2/2}_0 5 - 8y^2 + 2y^4 \)

Is this correct?

 

[MarkFL]

\(\displaystyle 2\pi \int ^\sqrt{2/2}_0 (3 - y^2)^2 - (3 - (1 - y^2)^2 dy \)

\(\displaystyle 2\pi \int^\sqrt{2/2}_0 9 - 6y^2 + y^4 - 3 + 1 + 2y^2 - y^4\)

\(\displaystyle = 2\pi \int^\sqrt{2/2}_0 5 - 8y^2 + 2y^4 \)

Is this correct?

Your upper limit should be \(\displaystyle \frac{1}{\sqrt{2}}\) or \(\displaystyle \frac{\sqrt{2}}{2}\).

Now, your integrand in the first line is correct, except for a missing closing bracket. After that you have made some algebra mistakes. You should initially have:

\(\displaystyle \left(3-y^2 \right)^2-\left(3-\left(1-y^2 \right) \right)^2\)

Now, let's first distribute the negative sign in the second term:

\(\displaystyle \left(3-y^2 \right)^2-\left(3-1+y^2 \right)^2\)

Collect like terms:

\(\displaystyle \left(3-y^2 \right)^2-\left(2+y^2 \right)^2\)

Expand:

\(\displaystyle \left(9-6y^2+y^4 \right)-\left(4+4y^2+y^4 \right)\)

Distribute negative sign and remove brackets:

\(\displaystyle 9-6y^2+y^4-4-4y^2-y^4\)

Collect like terms:

\(\displaystyle 5-10y^2=5\left(1-2y^2 \right)\)

And so you may state:

\(\displaystyle V=10\pi\int_0^{\frac{1}{\sqrt{2}}} 1-2y^2\,dy\)

 

[shamieh]

Thanks for helping me with my signs Mark. Seems like that was the hardest part of the whole problem lol.

so

\(\displaystyle 10 * (y - \frac{2y^3}{3}) | 0 to \frac{\sqrt{2}}{2}\)

\(\displaystyle \frac{30\pi\sqrt{2}}{6} - \frac{10\pi}{6} = \frac{10\pi\sqrt{2}}{3}\)

WOW! What a problem. Is this correct? I'm praying it is

 

[MarkFL]

Yes, that's correct:

\(\displaystyle V=10\pi\left[y-\frac{2}{3}y^3 \right]_0^{\frac{1}{\sqrt{2}}}= \frac{10\pi}{\sqrt{2}}\left(1-\frac{2}{3}\cdot\frac{1}{2} \right)= \frac{10\pi}{\sqrt{2}}\cdot\frac{2}{3}= \frac{20\pi}{3\sqrt{2}}= \frac{10\sqrt{2}\pi}{3}\)