What Does "Curl" Mean in Vector Fields?

[erocored]

That is how I understand curl:

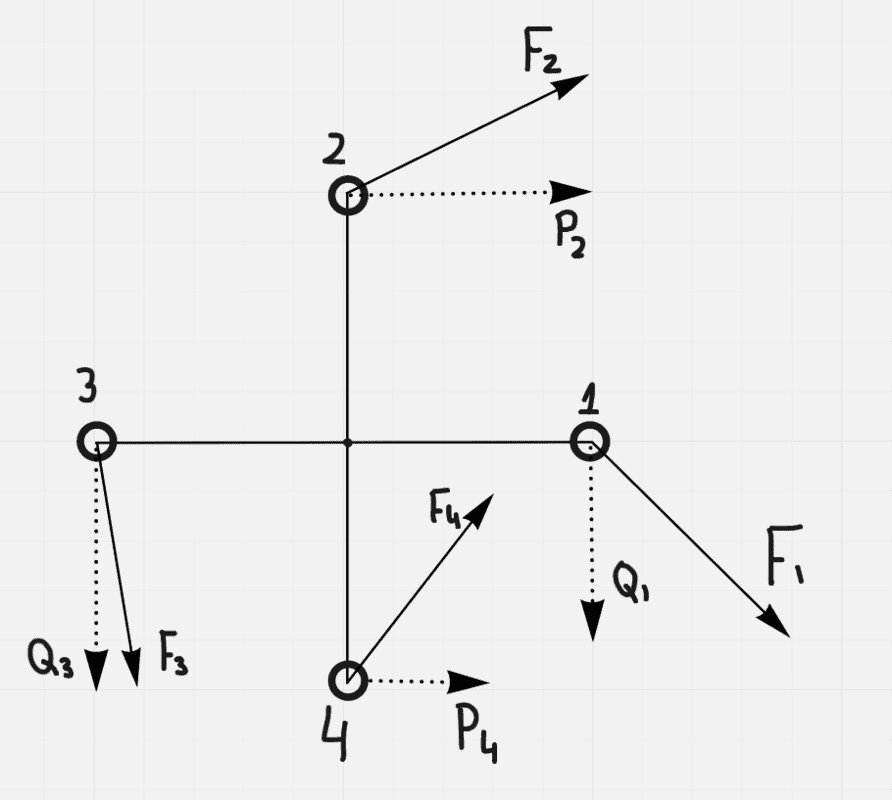
If I have a vane at some point $(x,y)$ of a vector field, then that vane will experience some angular velocities in points 1 $(x+dx,y)$, 2 $(x,y+dy)$, 3 $(x-dx,y)$, 4 $(x,y-dy)$. Adding those angular velocities gives me the resulting angular speed of this vane. But why is it important to know this resulting angular speed, what else does it give?

 

[jedishrfu]

Perhaps this will clarify things

https://betterexplained.com/articles/vector-calculus-understanding-circulation-and-curl/

 

[adnmcq]

Curl is how much a vector field (sorry for tautology) curls. The vector field representing water velocity as it circles down the drain has a big curl. Wind blowing eastward over some field would have near-zero curl. Chapter 1.2 of griffiths electrodynamics gives good explanation- he is extremely clear and curl is important in e and m. https://www.zackrauen.com/PublicFiles/School/Textbooks/Electrodynamics.pdf

 

[Eclair_de_XII]

The vector field representing water velocity as it circles down the drain has a big curl. Wind blowing eastward over some field would have near-zero curl.

From this statement, this is how I interpret curl:

Let's say you have a vector field. Now let's say you have some function that takes said vector field as its argument and returns the direction of the vector field at a given point. The curl is basically the derivative of that function with respect to the coordinates that the field is defined at.