What Does Reducing Z[x] Modulo the Prime Ideal (p) in Polynomial Rings Mean?

[Math Amateur]

I am reading Dummit and Foote Section 9.2: Polynomial Rings Over Fields I

I am having some trouble understanding Example 3 on page 300 (see attached)

My problem is mainly with understanding the notation and terminology.

The start of Example 3 reads as follows.

"If p is a prime, the ring Z/pZ[x] obtained by reducing Z[x] modulo the prime ideal (p) is a Principal Ideal Domain, since the coefficients lie in the field Z/pZ ... ... "

To me the ring Z/pZ[x] would be formed by reducing Z modulo p to form three cosets, namely

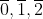and then forming Z/pZ[x] by taking coeffiients from Z/pZ

I am really unsure what D&F mean by "reducing Z[x] modulo the prime ideal (p)" unless they mean reducing the coefficients of Z[x] to coefficients from Z/pZ.

I am also assuming that when D&F use the notation Z/pZ[x] they are meaning (Z/pZ)[x]Can someone clarify this for me?

Peter

 

[Fernando Revilla]

I am really unsure what D&F mean by "reducing Z[x] modulo the prime ideal (p)" unless they mean reducing the coefficients of Z[x] to coefficients from Z/pZ.

I am also assuming that when D&F use the notation Z/pZ[x] they are meaning (Z/pZ)[x]

I am pretty sure they mean just what you say, the polynomial ring $(\mathbb{Z}/p\mathbb{Z})[x]$ or with other notations, $\mathbb{Z}_p[x]$ or $\left(\mathbb{Z}/(p)\right)[x]$.