- #1
pkc111
- 225
- 26
- Homework Statement
- State the work-energy theorem.
- Relevant Equations
- see below
My research leads to 2 slightly different equations. See equations 1 and 2 attached.
Also, for equation 1 should Wext be Wnet ext ?
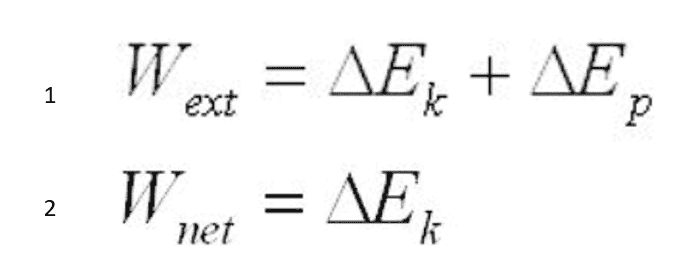
Also, for equation 1 should Wext be Wnet ext ?