- #1
hyperddude
- 15
- 0
To anyone who saw my previous thread, yes, this is quite similar to it  .
.
Given a rectangle, say a painting, with with mass [itex]m[/itex], height [itex]h[/itex], and width [itex]w[/itex] with two point supports to a wall at its two upper corners, what force does each support exert?
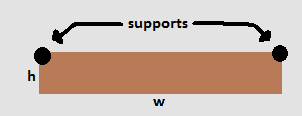
Moment of inertia of a rectangle about its center: [itex]\frac{m(h^2+w^2)}{12}[/itex]
Moment of inertia of a rectangle about a corner: [itex]\frac{m(h^2+w^2)}{3}[/itex]
^Not sure if those equations will be relevant
Common sense and intuition tells us that the vertical component from each support will be [itex]mg/2[/itex]. But is there a horizontal component? That's what I'm trying to find out. One solution I had in mind was to break the [itex]mg[/itex] downward force into components and try setting them as the forces by the pivots, but I ended up just going in circles.
Homework Statement
Given a rectangle, say a painting, with with mass [itex]m[/itex], height [itex]h[/itex], and width [itex]w[/itex] with two point supports to a wall at its two upper corners, what force does each support exert?
Homework Equations
Moment of inertia of a rectangle about its center: [itex]\frac{m(h^2+w^2)}{12}[/itex]
Moment of inertia of a rectangle about a corner: [itex]\frac{m(h^2+w^2)}{3}[/itex]
^Not sure if those equations will be relevant
The Attempt at a Solution
Common sense and intuition tells us that the vertical component from each support will be [itex]mg/2[/itex]. But is there a horizontal component? That's what I'm trying to find out. One solution I had in mind was to break the [itex]mg[/itex] downward force into components and try setting them as the forces by the pivots, but I ended up just going in circles.