What Happens After an Elastic Glancing Collision Between Two Unequal Masses?

[bingo92]

1. Homework Statement [/b]
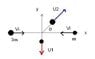
Two particles with masses m and 2m are moving toward each other along the x-axis with the same initial speeds vi. Particle m is traveling to the left, while particle 3m is traveling to the right. They undergo an elastic glancing collision such that particle m is moving downward after the collision at right angles from its initial direction.
A)Find the final speeds of the two particles.
B) What is the angle theta at which the particle 3m is scattered?

I know momentum is conserved as well as kinetic energy. I also know that i must separate the momentum before and after into i-hat and j-hat components but i just can't set up the answer. I've been going at this for quite a few hours and I just want to see how its done so i can go to bed peacefully.

Is this suppose to be a "challenging" question or should steer away from physics past 1st year uni.

 

[Quinzio]

I also know that i must separate the momentum before and after into i-hat and j-hat components but i just can't set up the answer.

You can separate the speeds in the same way before the collision.
Of course this separations will be done in a useful way.
How can you split the speed vector in two parts ?
Which angle between the two parts ? Which angle wrt to the original speed ?

Another way that may be simpler is to "play" wrt the center of mass.

 

[ehild]

Instead of fighting with formulas for hours, just make a drawing (something like the attached picture) and everything will be clear. By the way, is the mass of the second particle 2m or 3m?
You know it well, the kinetic energy is conserved and both the x and y components of the momentum. What are these components of momentum for both bodies before and after the collision in terms of the initial speed (Vi) and the final ones (U1,U2) and the angle theta?


ehild

 

[ashishsinghal]

Since you already know the facts I would suggest that you show the attempt so that we may correct you

 

[rwisz]

I understand that this question may be challenging for you and I appreciate your persistence in trying to solve it. I will provide a step-by-step solution to help you understand the concept better.

First, let's define the initial momentum of particle m as P1 and the initial momentum of particle 3m as P2. Since the particles have the same initial speed vi, their initial momenta are equal in magnitude but opposite in direction, so P1 = -P2.

Next, we can use the conservation of momentum to set up the following equation:

P1 + P2 = P1' + P2'

where P1' and P2' are the final momenta of the particles after the collision.

Since particle m is moving downward at a right angle from its initial direction, its final momentum P1' will have a j-hat component and no i-hat component. This means that P1' = P1j-hat.

On the other hand, particle 3m will be scattered at an angle theta, so its final momentum P2' will have both i-hat and j-hat components. We can express this as P2' = P2cos(theta)i-hat + P2sin(theta)j-hat.

Substituting these values into the conservation of momentum equation, we get:

P1 + P2 = P1j-hat + P2cos(theta)i-hat + P2sin(theta)j-hat

Since P1 = -P2, we can rewrite this as:

-P2 + P2 = P1j-hat + P2cos(theta)i-hat + P2sin(theta)j-hat

Simplifying, we get:

P2cos(theta) = P1 and P2sin(theta) = P2

Now, we can use the conservation of kinetic energy to set up another equation:

1/2mvi^2 + 1/2(2m)vi^2 = 1/2mv1'^2 + 1/2(2m)v2'^2

where v1' and v2' are the final speeds of particles m and 3m respectively.

Simplifying, we get:

(3/2)mvi^2 = (1/2)mv1'^2 + (1/2)mv2'^2

Since we know that v1' = 0 (particle m is moving