What happens to a ball placed on a moving conveyor belt?

[zenterix]

Homework Statement

Consider a conveyor belt moving with a constant velocity $\vec{v}_{g,c}$ relative to the ground reference frame. A ball of mass $m$ and radius $R$ is placed on the conveyor belt initially at rest relative to the ground frame. What happens to the ball? Assume there is friction due to contact forces between ball and conveyor belt.

Relevant Equations

Because there is a relative velocity between the conveyor belt and the ball, there is kinetic friction $f_k$ (see picture below).

$f_k$ accelerates the ball and causes rotation due to torque applied at contact point about center of mass (CM).

Torque equation
$$\vec{\tau}_{cm,ball}=Rf_k\hat{k}=I_{cm}\alpha_{cm}\hat{k}$$
$$\implies \vec{\alpha}_{cm}=\frac{Rf_k}{I_{cm}}\hat{k}$$

$2^{nd}$ Law Equation
$$f_k\hat{i}=ma_{g,cm}\hat{i}$$
$$\implies \vec{a}_{g,cm}=\frac{f_k}{m}\hat{i}$$

We can integrate $\vec{\alpha}_{cm}$ and $\vec{a}_{g,cm}$ to obtain angular and linear velocities

$$\vec{\omega}_{cm}=\frac{Rf_k t}{I_{cm}}\hat{k}$$
$$\vec{v}_{g,cm}=\frac{f_k}{m}t \hat{k}$$

Here is my depiction of the initial state:

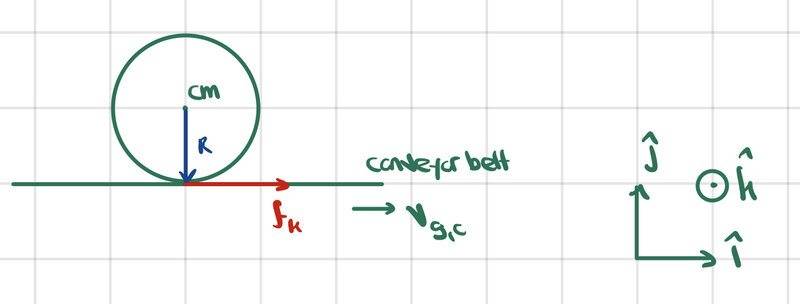
Note that the presence of $f_k$ means the ball is initially slipping. We also know that the linear and angular speeds of the ball are increasing in time. At some point, the ball should stop slipping.

The condition for no slipping is that the speed of the ball relative to the conveyor belt be the same as the arc length speed of rotation, ie

$$\vec{v}_{c,cm}=\vec{r}_{c,cm} \times \omega_{cm}=R\hat{j} \times \omega_{cm}\hat{k}$$
$$\implies \vec{v}_{c,cm}=-R\omega_{cm}\hat{i}$$

Notice the negative sign means that when not slipping, the ball's CM is still moving to the left relative to the conveyor belt.

But we also know
$$\vec{v}_{g,cm}=\vec{v}_{g,c}+\vec{v}_{c,cm}$$

$$\implies \vec{v}_{c,cm}=(\frac{f_k}{m}t-v_{g,c})\hat{i}$$

We see that initially, the relative speed of the ball's CM to the conveyor belt is just the negative of the speed of the conveyor belt, $v_{g,c}$, but because the ball is accelerating, this relative speed becomes less negative in time. At some point it must reach the relative speed associated with no slipping, $-R\omega_{cm}$.

Recall that

$$\vec{\omega}_{cm}=\frac{Rf_k t}{I_{cm}}\hat{k}$$

So when we equate our two expressions for $\vec{v}_{c,cm}$ we have

$$\frac{f_k}{m}t-v_{g,c} = -\frac{Rf_k t}{I_{cm}}$$

$$\implies t _{ns}= \frac{v_{g,c}}{\frac{f_k}{m}+\frac{f_k R^2}{I_{cm}}}$$

At $t_{ns}$ the point of contact between ball and conveyor belt is at rest and there is no friction any longer (kinetic nor static).

This represents a final state of static equilibrium.

Is this analysis correct?

 

[TSny]

Your work looks correct to me.

There is a minor typographical error in the second equation shown below, where $\hat k$ should be $\hat i$

We can integrate $\vec{\alpha}_{cm}$ and $\vec{a}_{g,cm}$ to obtain angular and linear velocities

$$\vec{\omega}_{cm}=\frac{Rf_k t}{I_{cm}}\hat{k}$$
$$\vec{v}_{g,cm}=\frac{f_k}{m}t \hat{k}$$

 

[TSny]

At $t_{ns}$ the point of contact between ball and conveyor belt is at rest and there is no friction any longer (kinetic nor static).

This represents a final state of static equilibrium.

I wouldn't call it static equilibrium. In the final state, the ball is spinning and the center of the ball has a nonzero translational velocity relative to the ground and a nonzero translational velocity relative to the belt. But it is a state of equilibrium in the sense that the net torque and net force on the ball are zero in the final state.

 

[zenterix]

What happens if we now make the conveyor belt inclined relative to the horizontal ground, such that there is a gravitational force component accelerating the ball?

Torque about CM is the same as before, so

$$\vec{\alpha}_{cm}=\frac{Rf_k}{I_{cm}}\hat{k}$$

$$\vec{\omega}_{cm}=\frac{Rf_k t}{I_{cm}}\hat{k}$$

$$\vec{v}_{g,cm}=\frac{f_k+mg\sin{\theta}}{m}t$$

The $2^{nd}$ law equation is different because there is now gravity helping to accelerate the CM

$$(f_k+mg\sin{\theta})\hat{i}=m\vec{a}_{g,cm}$$
$$\implies \vec{a}_{g,cm}=\frac{f_k+mg\sin{\theta}}{m}$$

No slipping (actually the ball is skidding) condition is the same as before:

$$\vec{v}_{c,cm}=-R\omega_{cm} \hat{i}$$

As before we have

$$\vec{v}_{c,cm}=\vec{v}_{g,cm}-\vec{v}_{g,c}=\frac{f_k+mg\sin{\theta}t}{m}\hat{i}-v_{g,c}\hat{i}$$

When we equate the two previous expressions (subbing in for $\omega_{cm}$ and solve for $t$ we obtain

$$t_{ns}=\frac{v_{g,c}}{\frac{f_k+mg\sin{\theta}}{m}+\frac{R^2 f_k}{I_{cm}}}$$

And this $t_{ns}$ is smaller than the one we found previously for the horizontal conveyor belt. So the ball takes less time to reach no slipping velocity. However, $mg\sin{\theta}$ is still present and it continues accelerating the ball.

From this point on (ie, from $t_{ns}$ on, we can't use the equations we've been using so far because kinetic friction is present once more, but in the opposite direction. The presence of kinetic friction is determined by the relative velocity of the contact point of the ball relative to the conveyor belt being non-zero.

Up to this point, this relative velocity was negative (relative to the ground, the conveyor belt was moving faster in the positive direction than the ball), but right after the no slipping condition is achieved, the relative velocity becomes positive, ie the ball is moving faster in the positive $\hat{i}$ direction than the conveyor belt.

$$\vec{\tau}_{cm,ball}=-R\hat{j} \times (-f_k \hat{i}) = -Rf_k \hat{k} = I_{cm} \alpha_{cm} \hat{k}$$
$$\implies \vec{\alpha}_{cm}=\frac{-Rf_k}{I_{cm}}\hat{k}$$

$$\vec{\omega}_{cm}=(\omega_{ns}-\frac{Rf_k t}{I_{cm}})\hat{k}$$

Note that there is now an initial angular velocity $\omega_{ns}$ which is the angular velocity at the no slipping point derived earlier. Notice that from this point onwards, angular velocity decreases in time without bound, ie the ball's rotation will eventually change orientation.

Using the $2^{nd}$ law we have

$$(mg\sin{\theta}-f_k)\hat{i}=ma_{g,cm} \hat{i}$$

$$\implies \vec{a}_{g,cm}=\frac{mg\sin{\theta}-f_k}{m}\hat{i}$$

$$\implies \vec{v}_{g,cm}=(v_{g,cm,ns}+\frac{mg\sin{\theta}-f_k}{m}t)\hat{i}$$

Where $v_{g,cm,ns}$ is the initial velocity of CM in the ground frame. This is simply the velocity of CM relative to ground in the no slipping state we derived previously. Note that this velocity is increasing in time, but the acceleration is now smaller than before the no slipping condition was met, because before kinetic friction was helping gravity, and now it is opposing gravity.

Finally, let's just show that in fact the contact point will now have a positive velocity relative to the conveyor belt. We want to calculate

$$\vec{v}_{c,cp}=\vec{v}_{cm,cp}-\vec{v}_{cm,c}=\vec{v}_{cm,cp}+\vec{v}_{c,cm}$$

So let's first figure out what $\vec{v}_{c,cm}$ and $\vec{v}_{cm,cp}$ are

$$\vec{v}_{c,cm}=\vec{v}_{g,cm}-\vec{v}_{g,c}$$
$$=(v_{g,cm,ns}+\frac{mg\sin{\theta}-f_k}{m}t)\hat{i} - v_{g,c}\hat{i}$$$$\vec{v}_{cm,cp}=\vec{\omega}_{cm} \times \vec{r}_{cm,cp}$$
$$=(\omega_{ns}-\frac{Rf_k t}{I_{cm}})\hat{k} \times (-R\hat{j})$$
$$=(R\omega_{ns}-\frac{R^2f_k t}{I_{cm}})\hat{i}$$

Now we can sub in and obtain $\vec{v}_{c,cp}$, the velocity of the contact point of the ball relative to the conveyor belt

$$\vec{v}_{c,cp}=(R\omega_{ns}-\frac{R^2f_k t}{I_{cm}})\hat{i}+(v_{g,cm,ns}+\frac{mg\sin{\theta}-f_k}{m}t)\hat{i} - v_{g,c}\hat{i}$$
$$=(R\omega_{ns}-\frac{R^2f_k}{I_{cm}}t+v_{g,cm,ns}+\frac{mg\sin{\theta}-f_k}{m}t-v_{g,c})\hat{i}$$

Now we can differentiate the latter expression to obtain the acceleration of the contact point of the ball with the conveyor belt, relative to the conveyor belt.
$$\vec{a}_{c,cp}=\frac{R^2f_k}{I_{cm}}+\frac{mg\sin{\theta}-f_k}{m}$$
$$=f_k(\frac{R^2}{I_{cm}}-\frac{1}{m})+g\sin{\theta}$$

Now we can use $I_{cm}=\frac{2}{5}mR^2$ for the moment of inertia of a solid sphere to obtain

$$\vec{a}_{c,cp}=f_k\frac{3}{2m}+g\sin{\theta}>0$$

Note that $\vec{v}_{c,cp}$ starts at zero when the ball is not slipping, and as we just saw $\vec{a}_{c,cp}$ is positive, so $\vec{v}_{c,cp}$ immediately becomes positive after reaching the no slipping point, and hence there is a relative velocity of contact point relative to conveyor belt, and kinetic friction appears in the direction opposite the relative velocity.

 

[zenterix]

I wouldn't call it static equilibrium. In the final state, the ball is spinning and the center of the ball has a nonzero translational velocity relative to the ground and a nonzero translational velocity relative to the belt. But it is a state of equilibrium in the sense that the net torque and net force on the ball are zero in the final state.

You are right, it is not in static equilibrium. But actually the net force on the ball is not zero I just realized.

I am using a specific definition of static equilibrium I saw in the notes to MIT 8.01 on MIT OCW about static equilibrium in rotational motion. That definition is that there are two sufficient and necessary conditions for a rigid body to be in static equilibrium:

1) The sum of forces acting on the rigid body is zero
$$\sum_{i=1}^{n} \vec{F}_i = \vec{0}$$

2) The vector sum of torques about any point S in the rigid body is zero
$$\sum_{i=1}^{n} \vec{\tau}_{S,i}$$

When there is no slipping there is no torque, but there is still a component of gravity $mg\sin{\theta}$ accelerating the ball, ie the sum of forces acting on the ball is not zero.

 

[zenterix]

You are right, it is not in static equilibrium. But actually the net force on the ball is not zero I just realized.

I am using a specific definition of static equilibrium I saw in the notes to MIT 8.01 on MIT OCW about static equilibrium in rotational motion. That definition is that there are two sufficient and necessary conditions for a rigid body to be in static equilibrium:

1) The sum of forces acting on the rigid body is zero
$$\sum_{i=1}^{n} \vec{F}_i = \vec{0}$$

2) The vector sum of torques about any point S in the rigid body is zero
$$\sum_{i=1}^{n} \vec{\tau}_{S,i}$$

When there is no slipping there is no torque, but there is still a component of gravity $mg\sin{\theta}$ accelerating the ball, ie the sum of forces acting on the ball is not zero.

Ok, I confused myself! The above actually refers to the second case, where the conveyor belt is inclined. With regards to the first case of a horizontal conveyor belt you were 100% correct, the sums of forces and torques acting on the body are both zero, so in that sense there is static equilibrium.

 

[zenterix]

Up to this point, this relative velocity was negative (relative to the ground, the conveyor belt was moving faster in the positive direction than the ball), but right after the no slipping condition is achieved, the relative velocity becomes positive, ie the ball is moving faster in the positive i direction than the conveyor belt.

I believe there was a mistake in my reasoning here. Let me recall the supposed facts here

- There is torque due to a friction force, so we can calculate angular acceleration. I will use the notation $f_f$ for friction force because at this point I am going to refrain from concluding whether it is kinetic or static
$$\vec{\alpha}_{cm}=\frac{-Rf_f}{I_{cm}}\hat{k}$$

- We can integrate to obtain angular velocity, noting that there is an initial angular velocity that we know from having calculated the angular velocity at which no slipping occurs.

$$\vec{\omega}_{cm}=(\omega_{ns}-\frac{Rf_f t}{I_{cm}}\hat{k})$$

- The $2^{nd}$ law gives us linear acceleration relative to the ground frame

$$\vec{a}_{g,cm}=\frac{mg\sin{\theta}-f_f}{m}\hat{i}$$

$$\vec{v}_{g,cm}=(v_{g,cm,ns}+\frac{mg\sin{\theta}-f_f}{m}t)\hat{k}$$

What is the no slipping condition now?

$$\vec{v}_{c,cm}=-\vec{v}_{cm,cp}=-\omega_{cm}\hat{k} \times (-R\hat{j})=-R\omega_{cm}\hat{i}$$
$$\implies \vec{v}_{c,cm}=-R(\omega_{ns}-\frac{Rf_f t}{I_{cm}})\hat{i}$$

In problems where the conveyor belt isn't moving, the above expression would be for $v_{g,cm}$, which we could integrate to get another expression for $a_{g,cm}$ and use to solve for the value of the friction force necessary to make all our equations balance.

Here we must calculate $\vec{v}_{g,cm}$ ourselves.

$$\vec{v}_{g,cm}=\vec{v}_{g,c}+\vec{v}_{c,cm}=v_{g,c}\hat{i}-R(\omega_{ns}-\frac{Rf_f t}{I_{cm}})\hat{i}$$
$$=(v_{g,c}-R(\omega_{ns}-\frac{Rf_f t}{I_{cm}}))\hat{i}$$

At this point, we have two equations specifying what $\vec{v}_{g,cm}$ is. We can equate them and solve for $f_f$. At first glance it seems that the equations involve $t$ and so $f_f$ will be a function of time, but it seems this is not the case, ie there is a constant level of friction that generates no slipping.

$$v_{g,c}-R(\omega_{ns}-\frac{Rf_f t}{I_{cm}})=v_{g,cm,ns}+\frac{mg\sin{\theta}-f_f}{m}t$$

$$\implies f_f=\frac{mgI_{cm}\sin{\theta}}{I_{cm}+mR^2}$$

One interesting thing to note is that the no slipping condition is actually saying that the relative speed of the contact point of the ball relative to the conveyor belt is zero.

$$\vec{v}_{c,cm}=-\vec{v}_{cm,cp} \implies \vec{v}_{c,cm}+\vec{v}_{cm,cp}=\vec{0}$$

But

$$\vec{v}_{c,cp}=\vec{v}_{c,cm}+\vec{v}_{cm,cp}=\vec{0}$$

Also, if we differentiate $\vec{v}_{c,cp}$ we obtain

$$\vec{a}_{c,cp}=-\frac{R^2 f_f}{I_{cm}}+\frac{mg\sin{\theta}-f_f}{m}=\frac{mgI_{cm}\sin{\theta}}{mI_{cm}}-\frac{R^2m+I_{cm}}{mI_{cm}}f_f$$

This is a decreasing linear function of $f_f$. When $f_f=\frac{mgI_{cm}\sin{\theta}}{I_{cm}+mR^2}$ this acceleration is zero, but if $f_f$ is below this level, acceleration of the contact point relative to the conveyor belt is positive, and the analysis from my previous post is valid (I think), ie there will be kinetic friction.

Whether friction is high enough to sustain the no slipping or not depends on the coefficient of friction of the conveyor belt; if it is not high enough, the ball will slip.

To conclude let me address the type of friction involved here. If $f_f=\frac{mgI_{cm}\sin{\theta}}{I_{cm}+mR^2}$ then there is no slipping and the friction is static. Otherwise, the friction is kinetic. The ball will roll down the conveyor belt without slipping, with increasing angular and linear velocity.

 

[TSny]

I think your analysis is good. Nice work.

I agree with your expression for the magnitude of the friction force that will maintain rolling without slipping. As you say, from this you can work out the minimum coefficient of static friction that is necessary to provide rolling without slipping. For a solid, uniform ball I find that $\mu_{s, min} = \frac{2}{7} \tan \theta$.

I found it easier to work in the frame of reference of the belt, which is an inertial frame. The forces, torques, angular acceleration of the ball, angular velocity of the ball, and acceleration of the cm of the ball have the same value in the belt frame and the ground frame. Transforming the velocity of the cm of the ball between the belt frame and the ground frame is easy.

 

[TSny]

I am using a specific definition of static equilibrium I saw in the notes to MIT 8.01 on MIT OCW about static equilibrium in rotational motion. That definition is that there are two sufficient and necessary conditions for a rigid body to be in static equilibrium:

1) The sum of forces acting on the rigid body is zero
$$\sum_{i=1}^{n} \vec{F}_i = \vec{0}$$

2) The vector sum of torques about any point S in the rigid body is zero
$$\sum_{i=1}^{n} \vec{\tau}_{S,i}$$

The MIT document states the following:

My interpretation of this is that they are defining "static equilibrium of an extended object" to mean that there exists an inertial reference frame for which the center of mass of the body remains at rest and the body does not rotate. A ball rolling without slipping on a horizontal surface does not meet this definition of static equilibrium since there does not exist an inertial frame for which the ball is not rotating.

A block sliding with constant velocity on a frictionless, horizontal surface would be in static equilibrium according to this definition.

I might be misinterpreting their statement. They might be saying that the term "static equilibrium" should only be used in the particular inertial frame for which the cm of the body is at rest and the body is not rotating. In this case, the sliding block is not in static equilibrium except in the frame moving with the block. Anyway, this is not too important in my opinion since it's a matter of how you want to define "static equilibrium".