What Happens to the Velocities in a Frictionless Curved Surface System?

[Nikhil Kumar]

A small body of mass m placed over a larger mass M whose surface is horizontal near the smaller mass and gradually curves to become vertical. The smaller mass is pushed on the longer one at a speed v and the system is left to itself. Assume all surfaces to be frictionless. (Please refer the attached diagram).

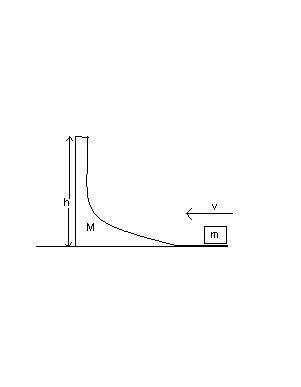
a) Find the speed of the larger block when the smaller block is sliding on the vertical part.

b) Find the speed of the smaller mass when it breaks off the larger mass at height h.

2. Homework Equations

Principle of conservation of linear momentum
Law of conservation of energy

3. The Attempt at a Solution

I have correctly solved the first part of the question. Here it goes:
Let velocity of larger block (M) when smaller block (m) reaches the vertical part be V, then by conservation of linear momentum ( I've taken the smaller mass + larger mass as system):

Initial linear momentum of system = final linear mom. of system
» mv + 0 = (M + m)V
» V = mv / (M+m) (This is correct)

However, i am stuck at the second part. I tried it attempting like this:

Taking the smaller mass as the system, initial energy of the system= ½ mv²
Let v₁ be the vel. of the smaller mass ( with respect to ground) when it breaks off from the vertical mass, then total energy at this instant = ½ mv₁² + mgh (assuming PE = 0 at ground level)

As no external force acts on the system, the mech. energy is conserved, hence:
Intial Mechanical energy = Final Mechanical energy
» ½ mv² = ½ mv₁² + mgh
» v₁ = [v² - 2gh]^1/2

But this is wrong! What is the fallacy in my logic?

Another allied question: Suppose a frame of reference is moving with a const. velocity v wrt ground. A body of mass m moves with a const. vel. V wrt the frame of reference. then what is its kinetic energy? Which vel. should we take for calculating KE? Like PE, is KE also relative?

Thanks.

 

[mal4mac]

Can you take the smaller mass "as the system"? Try looking at the whole system, including the larger mass before and after...

 

[Nikhil Kumar]

Thanks sir! This has solved my problem. I solved it like this:
Let v₁ be the velocity of the smaller mass wrt the ground when it just flies away from the larger mass. Taking 'the larger mass + smaller mass as the system' and applying law of cons. of energy, we have:

Intial energy = Final energy
½ mv² = ½ MV² + ½ mv₁² + mgh

Hence, v₁ = {[(m² + Mm + m²)/(M+m)²]-2gh}^1/2

Thanks sir.

 

[Nikhil Kumar]

Another allied question: Suppose a frame of reference is moving with a const. velocity v wrt ground. A body of mass m moves with a const. vel. V wrt the frame of reference. then what is its kinetic energy? Which vel. should we take for calculating KE? Like PE, is KE also relative?

Thanks.

What is the answer to this question?

 

[mal4mac]

Nikhil - thanks you for introducing an interesting problem and doing most of the hard work. And don't call me sir! It makes me feel old Just Mal will do.

On "the frame of reference" thing. If K is directly proportional to v squared, and v is (obviously) relative then...

 

[ritwik06]

Thats a question from HC Verma. Hey Nikhil, ar you Nikhil Kumar Singh from CMS Aliganj?

 

[Nikhil Kumar]

Thanks Mal! You made my day.

And Ritwik, I'm not that Nikhil. I live in Chattisgarh.