JamesPaylow
- 16
- 3
- TL;DR Summary
- A hypothetical experimental setup is depicted, can you help me understand what would happen in the scenarios described here?
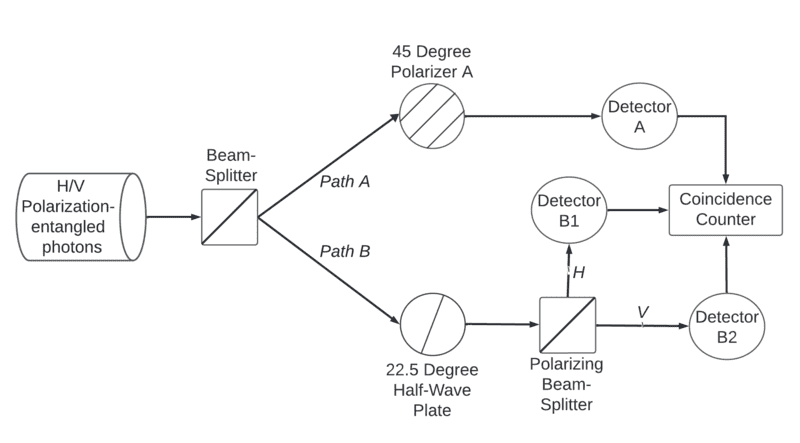
Please consider the depicted setup. We assume that the source is producing only H/V polarization entangled photon pairs (which is separately confirmed prior to the experiment).
Scenario 1) First suppose that the depicted 45 Degree Linear Polarizer A is absent. Photon B's polarization is in H/V superposition to start, then after going through the half wave plate oriented at 22.5 degrees -> (V)ertical polarization becomes (D)iagonal and (H)orizontal polarization becomes (A)ntidiagonal. The Polarizing Beam Splitter transmits V and reflects H. If A and D encounter the PBS they are each randomly converted and routed towards either the H or V path. Detectors B1 and B2 should register roughly the same number of photons after reducing to coincidences with Detector A.
Scenario 2) As depicted, the 45 Degree Linear Polarizer A is present. Photon A encounters the diagonally (45 degree) oriented linear polarizer in Path A. Since the photons in Path A and Path B are orthogonally polarized and entangled, when Photon A goes through the diagonal polarizer then we know that Photon B is (A)ntidiagonally polarized, and the particles are thereafter no longer entangled. If Photon B is A polarized when approaching the HWP oriented at 22.5 degrees, then it becomes (H)orizontally polarized. H polarization is reflected through the PBS. As a result, only Detector B1 registers impact (after filtering to coincides along Path A using the coincidence counter).
Have I described this correctly? If so, could the length of Path B change the outcome?
I'm familiar with the Quantum Eraser experiment and how in that experiment they showed that the length of the paths did not matter, but I think that post-selection filtering used to reduce the diffraction pattern to an interference pattern could possibly explain what seems to be retrocasual effect. Since the setup depicted here doesn't use interference patterns I think the same explanation would not apply.
@vanhees71 @gentzen an extension of my previous question :) Thanks in advance!
Scenario 1) First suppose that the depicted 45 Degree Linear Polarizer A is absent. Photon B's polarization is in H/V superposition to start, then after going through the half wave plate oriented at 22.5 degrees -> (V)ertical polarization becomes (D)iagonal and (H)orizontal polarization becomes (A)ntidiagonal. The Polarizing Beam Splitter transmits V and reflects H. If A and D encounter the PBS they are each randomly converted and routed towards either the H or V path. Detectors B1 and B2 should register roughly the same number of photons after reducing to coincidences with Detector A.
Scenario 2) As depicted, the 45 Degree Linear Polarizer A is present. Photon A encounters the diagonally (45 degree) oriented linear polarizer in Path A. Since the photons in Path A and Path B are orthogonally polarized and entangled, when Photon A goes through the diagonal polarizer then we know that Photon B is (A)ntidiagonally polarized, and the particles are thereafter no longer entangled. If Photon B is A polarized when approaching the HWP oriented at 22.5 degrees, then it becomes (H)orizontally polarized. H polarization is reflected through the PBS. As a result, only Detector B1 registers impact (after filtering to coincides along Path A using the coincidence counter).
Have I described this correctly? If so, could the length of Path B change the outcome?
I'm familiar with the Quantum Eraser experiment and how in that experiment they showed that the length of the paths did not matter, but I think that post-selection filtering used to reduce the diffraction pattern to an interference pattern could possibly explain what seems to be retrocasual effect. Since the setup depicted here doesn't use interference patterns I think the same explanation would not apply.
@vanhees71 @gentzen an extension of my previous question :) Thanks in advance!
Last edited by a moderator:
 .
.
