What I consider to be a very hard spring-potential energy problem

[Patdon10]

Homework Statement

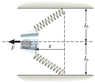
A horizontal slingshot consists of two light, identical springs (with spring constants of 57 N/m) and a light cup that holds a 1-kg stone. Each spring has an equilibrium length l0 = 47 cm. When the springs are in equilibrium, they line up vertically. Suppose that the cup containing the mass is pulled to x = 0.8 m to the left of the vertical and then released.

(a) Determine the system's total mechanical energy.
(b) Determine the speed of the stone at x = 0.

Homework Equations

Potential Elastic Energy: PE = (1/2)kx²
Conservation of energy: 1/2mv² + (1/2)kx² = 1/2mv² + (1/2)kx²

The Attempt at a Solution

This is really tough for me. I'm really not sure how to approach this.

Starting with problem a...
There are two springs and the system is not in motion initially. We know that total mechanic energy is change in K + change in PE.

The equation would be E = (0) + kx² = (57)(.8) = 45.6 J note I didn't make it (1/2)kx^2 because there are 2 springs.

This is not the correct answer. Any help would be appreciated.

 

[PhanthomJay]

Don't forget to square x, but x is not 0.8. The springs stretch more than that, use some geometry to calculate the change in length of the springs.

 

[Patdon10]

Oh, wow. You are totally right. I didn't think that the change in x would be in the diagonal direction.

so it would be:
sqroot(0.47² + 0.8²) = 0.9278 m

(57)(0.9278)² = 49.066 J

However, that is still the wrong answer : /
What am I missing?

Edit: You told me to find the change in x, and that's not what I was doing. Instead it should be
0.9278 - 0.47 = 0.4578 m

0.4578²*57 = 11.96 J. That is the correct answer for a. : )

Now to part B:
there is no initial kinetic energy, but there is definitely final kinetic energy. Also, at the end of the equation. There is no final PE, so it would be 0. I feel like I should use the conservation of energy here. What I have is:

0 + 0.4578²*57 = (1/2)mv² + 0
solving for this, I get v = 4.89 m/s. This is the right answer again. Thanks for the help!

 

[PhanthomJay]

Yes, nice work

 

[lonewolf219]

Hi, I am working on a very similar problem. I was wondering why the stone in the cup is not considered in the total mechanical energy of the system, when it seems to have potential energy?

 

[PhanthomJay]

You make a good observation, but it is not the gravitational PE that it is important, since it is referenced to an arbitrary axis, but rather, the change in gravitational PE that matters, as the the stone moves from its initial position to its 'final' position at x = 0, assuming that the slingshot is in a vertical plane. In this problem, this change is small, which would not be the case for example, if the stone had a very large mass much greater than 1 kg. Good point.