What is a focal length of a thin convex lens?

[Lotto]

Homework Statement

A thin convex lens is placed in an opaque bracket perpendicular to the optical axis. Behind the lens is at distance $L$ perpendicular to the optical axis built
a shade. A thin beam of light parallel to the optical axis hits the lens and
creates a point image on the shade. When we move the lens by a distance of $\delta$
in a direction perpendicular to the optical axis, the image of the point on the shade moves by a distance $\Delta$. Calculate the focal length of the lens.

Relevant Equations

$\frac{\Delta}{L}=\frac{\delta}{f}$

I think that there might be several solutions. I drawed one possible situation:

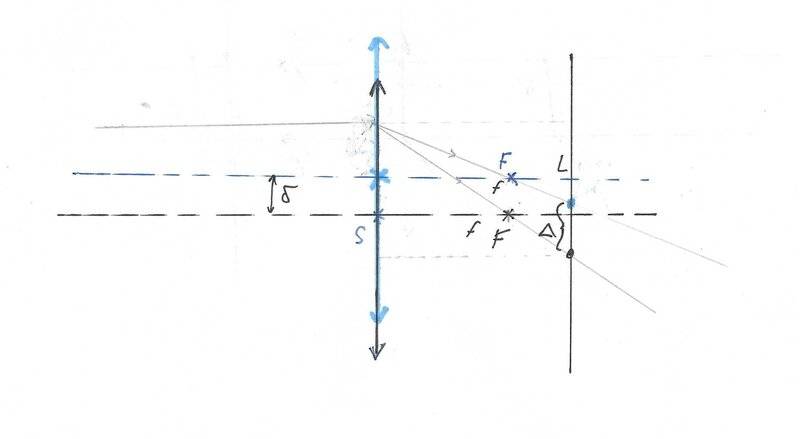
I think that this is just geometry, but I don't know how to solve it simply.

I had an idea that if the beam was going through the black axis, then it would be easy to calculate, and that would be aslo solution for all other cases. I mean that it doesn't matter where the beam is located with respect to the lens.

Then I calculated the focal lenght to be $f=L\frac{\delta}{\Delta}$ just from a triangle similarity, see "Relevant equations".

Is this thought correct? If not, could you give me a hint for the case drawed above?

 

[haruspex]

I calculated the focal lenght to be $f=L\frac{\delta}{\Delta}$ just from a triangle similarity, see "Relevant equations".

Look fine to me.

 

[Lotto]

Look fine to me.

So it is not dependent on a position of the beam, it doesn't matter if the beam goes initially through the optical axis or goes above it, the solution is only one.

But why? How to explain it? Intuitivelly, it makes quite sense, but physically?

 

[haruspex]

So it is not dependent on a position of the beam, it doesn't matter if the beam goes initially through the optical axis or goes above it, the solution is only one.

But why? How to explain it? Intuitivelly, it makes quite sense, but physically?

Have you tried drawing the diagram for L<f?

 

[hutchphd]

But why? How to explain it? Intuitivelly, it makes quite sense, but physically?

How does a lens work? It is designed so that any paraxial ray of light incident upon it will be bent to go through the focus. We are presumably aiming at a point source very far away, so that any intercepting ray is effectively paraxial. Therefore it must go through the backside focus if it hits the lens

 

[Lotto]

Have you tried drawing the diagram for L<f?

Now I have done it and the focal lenght is still given by $f=L\frac{\delta}{\Delta}$.

 

[Lotto]

Sorry for asking that late, but it came to my mind that I have no explanation for that $\Delta$ being the same no matter where the rays are relative to the axis.

If a ray lies in the optical axis, then $\Delta$ should be the same for a different ray that doesn't lie there. Both are parallel to the axis of course.

I am trying to prove it by using geomtery but I don't know how. It might be useful to know that if the deltas are the same, then areas of triangles (see the triangle above in my picture) should have the same areas.

Intuitivelly, it is "obvious", but how to prove it? I am asking because it is quite important in this problem. I don't need to prove it, but I find it interesting.

 

[kuruman]

For each of the refracted rays you can write straight-line equations taking the origin at the point of incidence on the lens:
$y_1=m_1x$
$y_2=m_2x$
Subtract to get $y_2-y_1=(m_2-m_1)x.$
It follows that
$\delta = (m_2-m_1)f$
$\Delta = (m_2-m_1)L$
Divide and solve for $f$.

 

[Lotto]

For each of the refracted rays you can write straight-line equations taking the origin at the point of incidence on the lens:
$y_1=m_1x$
$y_2=m_2x$
Subtract to get $y_2-y_1=(m_2-m_1)x.$
It follows that
$\delta = (m_2-m_1)f$
$\Delta = (m_2-m_1)L$
Divide and solve for $f$.

Wow, that's cool!

 

[kuruman]

There is also a geometric proof.
Let ##H=~# the distance between the original optical axis and the screen (see figure below).
There are two relevant right triangles, ABD and ABC whose hypotenuses are the refracted rays.
If you draw a line perpendicular to the optical axis at the focal lengths, two additional right triangles are formed that are similar to the above. I did not label their vertices to avoid clutter.

The ratio of right sides of similar triangles ABD is $$ \frac{\Delta +y}{L}=\frac{H}{f}.\tag{1}$$ The ratio of right sides of similar triangles ABC is $$ \frac{y}{L}=\frac{H-\delta}{f}.\tag{2}$$Subtract equation (2) from (1).