What is a good basis for coupled modes in a resonator?

[Supantho Raxit]

TL;DR

When trying to solve the Hamiltonian for coupled modes, what set of commutating operators can we use?

Suppose, there is an electro-optical modulator that can couple the neighboring modes in an optical ring resonator. The Hamiltonian for the system

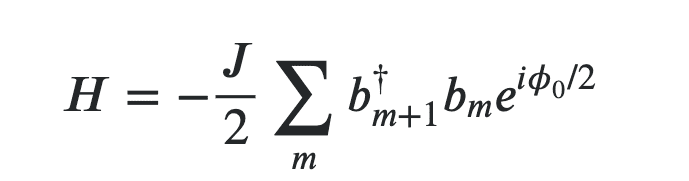
looks something like this^^ (see the attached image). Here we sum over all modes m and 𝜙0 is a parameter. What will be a good set of basis for the system? Suppose, we somehow restrict m to some upper bound m_max. What will be a good set of basis then?

 

[stevendaryl]

Since nobody else is answering... are the bs raising/lowering operators? Does the index m run through positive and negative integers?

 

[Supantho Raxit]

Yes, the b's are raising/lowering operators, and index m does run through positive and negative integers. The latter is a matter of choice since we can label our "sites" as we wish.