What is the acceleration of a car with a hanging mass at an angle of 23 degrees?

[GovernorBob]

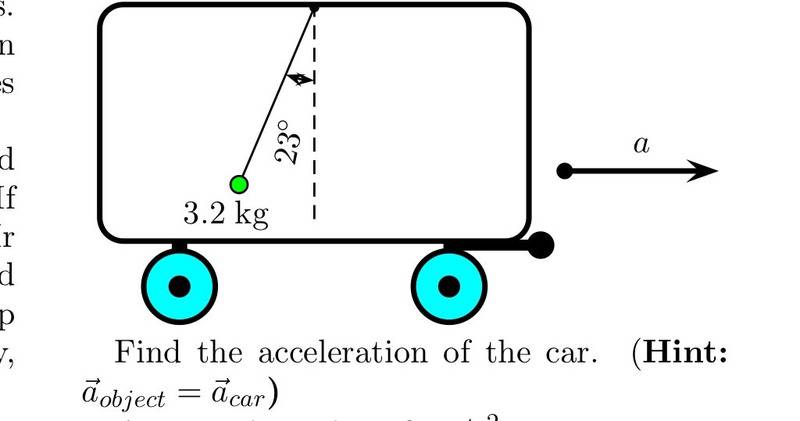
The problem states that a 3.4 kg object hangs at one end of a rope that is attached to a support on a car. The car and cruisin' and is accelerating, when it does this, the rope makes an angle of 23 degrees with the vertical. Acceleration of gravity is 9.8 m/s/s and the question is asking for the car's acceleration. A rad diagram for your visual

Equations
Σf= ma
Probably something with trig functions (sin, cos, tan)The first thing I did was multiply the mass 3.2 kg by gravity 9.2 m/s/s
That gave me a force of 31.36N, now, how do I use this to find the cars acceleration. I just don't see a correlation.

 

[Satvik Pandey]

Welcome to PF GovernorBob.
Do you know what is pseudo force?
The problem will be easier to solve if you consider a reference frame which is moving with the car and visualize the motion of that hanging mass wrt to that frame.