- #1
- 1,752
- 143
Let's say I have 3 lasers: A B and C. They are all at the same location in a room representing a 3D grid. I shine laser A at the wall, but not necessarily perpendicular to the wall. I shine laser B at the wall so that its beam forms the angle AB. I then shine laser C at the wall forming angle AC. Angle AC =AB, although B doesn't fall on the same spot on the wall as C. They both fall on a lotus of points forming a circle around point A since their angles from A are equal. I carefully measure the x, y, and z compoients of all 4 points:
P1: lasers' position
P2: beam A strikes the wall
P3: beam B strikes the wall
P4: beam C strikes the wall
I can find the angle AB with
arcos (A dot B) / (|A| |B|)
where A is the vector joining P1 and P2, and B is the vector joining P1 and P3.
And I can find the angle AC with the same method. These two angles equal each other. But how do I determine the angle of the arc between B and C on the lotus of points that surround point A?
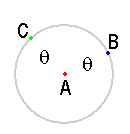
P1: lasers' position
P2: beam A strikes the wall
P3: beam B strikes the wall
P4: beam C strikes the wall
I can find the angle AB with
arcos (A dot B) / (|A| |B|)
where A is the vector joining P1 and P2, and B is the vector joining P1 and P3.
And I can find the angle AC with the same method. These two angles equal each other. But how do I determine the angle of the arc between B and C on the lotus of points that surround point A?
Last edited: