What Is the Angle Between the (111) and (1̅10) Planes in a Cubic Lattice?

In summary, the conversation involves identifying the (111) and ([11]0) planes in a cubic lattice and calculating the angle between them. The solution involves taking the angle between the normals to the planes to eliminate ambiguity. The person also mentions not being sure about the negative (110) and asks for thoughts on their drawing.
  • #1
Frinkz
8
0

Homework Statement


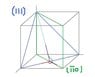
Indicate the (111) and ([11]0) ([11] has an over line, so is negative, don't know how to do on forums!) planes in a cubic lattice in a diagram, then calculate the angle between them.


The Attempt at a Solution


I think I have drawn this right (see attatchment), but I am not sure what angle it is referring to.

I would guess it is 90 degrees (in red), but I doubt I would be asked this, maybe the other angle (purple), could someone give any thoughts?

Also if my drawing is wrong, let me know! I wasn't 100% sure about the negative (110)
 

Attachments

  • lattice.jpg
    lattice.jpg
    24.4 KB · Views: 464
Physics news on Phys.org
  • #2
Take the angle between the normals to the planes. It will eliminate ambiguity and it will be much easier. You should know what vector is normal to the plan (h k l) if you studied reciprocal lattice.
 

FAQ: What Is the Angle Between the (111) and (1̅10) Planes in a Cubic Lattice?

What is the Quick Miller Index Lattice Problem?

The Quick Miller Index Lattice Problem is a mathematical problem that involves finding the Miller indices, which are a set of three integers used to define a crystallographic plane in a lattice. It is a fundamental concept in crystallography and is often used in materials science and engineering.

How is the Quick Miller Index Lattice Problem solved?

The Quick Miller Index Lattice Problem is typically solved using a combination of mathematical equations and visual interpretation. The Miller indices are determined by finding the reciprocal intercepts of the plane on the crystal lattice axes and taking their lowest common multiple. There are also software programs available that can quickly solve this problem.

Why is the Quick Miller Index Lattice Problem important?

The Quick Miller Index Lattice Problem is important because it allows scientists and engineers to accurately describe the crystal structure of a material. This information is crucial for understanding the physical and chemical properties of materials, as well as for designing and engineering new materials with specific properties.

What are some real-world applications of the Quick Miller Index Lattice Problem?

The Quick Miller Index Lattice Problem has many applications in materials science and engineering. It is used to determine the orientation of crystal structures in various materials, such as metals, ceramics, and semiconductors. This information is crucial for understanding the properties and behavior of these materials, which is important for designing new materials for various applications.

Are there any limitations to the Quick Miller Index Lattice Problem?

While the Quick Miller Index Lattice Problem is a powerful tool for describing crystal structures, it does have some limitations. For example, it does not account for defects or impurities in the crystal lattice, which can affect the properties of a material. Additionally, it is not applicable to non-periodic structures, such as amorphous materials. Therefore, it is important to use this method in conjunction with other characterization techniques for a complete understanding of a material's structure.

Similar threads

Solid State Physics - Miller Planes/Indices and Finding a
Replies
7
Views
3K
How Does Changing Lattice Dimensions Affect X-ray Scattering Angles?
Replies
1
Views
1K
Lattice constant, space between planes?
Replies
1
Views
1K
I What are the significant angles between intersecting planes in 4D space?
Replies
26
Views
2K
I Is it Possible to Index a Cubic Lattice with h^2+k^2+l^2=7?
Replies
1
Views
2K
I Understanding Ewald's sphere in the context of X-Ray diffraction
Replies
3
Views
4K
X-Ray Diffraction Homework: Find Lattice Spacing d
Replies
1
Views
2K
X-rays: Distance between WZ [1 0 3/2]surf layers in InAs
Replies
1
Views
1K
Particle subject to a hopping potential between two atoms in a lattice
Replies
4
Views
2K
What Is the Bravais Lattice Type and Miller Indices of This Crystal?
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top