What is the angle needed to see a distant point on a circle with a given radius?

[lubo]

Homework Statement

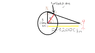
A circle with a radius (r) of 6000km.

From the centre of the circle to a point in the distance G where another person is standing is R = 40000 km.

Calculate the angle (θ) that the observer has to stand at point (O), to allow the observer to see the distant point G. If the observer stands at point N he cannot see point (G)

Point G can be visible by constructing a right angled triangle B O G and you should be able to use trigonometry.

Please see attached for the drawing. Sorry it is not the best quality. We have B at the centre of triangle, N is the top of the circle, O is the point the observer stands to see point G and G where the observer would like to see.

Homework Equations

SOH CAH TOA
A²=B²+C²
Triangles ad up to 180°

The Attempt at a Solution

you can find B - N - G (big triangle) from Pythagoras = √(40000² + 6000) = 40447.5 km.

For the triangle (BOG) where the observer stands and looks to G, because it is at an angle from the centre of the circle to (O) I am stuck how to calculate it.

Sine Rule cannot be used as I have no angles.

I could maybe use the Cosine rule c²= a²+b² - 2ab Cos C to find the angle.

C= cos^-1 ((-c² + a²+b²)/(2ab)) but the angle does not look like it is right angled so therefore I am not sure how I can work out O - G.

If I try and use a small triangle B - N - O -B then I have the same radius for both parts of the triangle and of course they will cancel out as c² - b² = a = Zero if both b and c are the same i.e. 6000.

I hope this makes sense as it is quite hard to explain as I cannot copy the picture.

 

[Nathanael]

Was that a replication of a given drawing? I don't think that drawing is correct.

The way I understood the problem is that you're trying to find the maximum angle where you can still see point G

Point O would not be the maximum point (you could go higher)
What do you think would be special about the highest point?

 

[lubo]

I am trying to find theta. This is at point O on the diagram. It is not really perfectly drawn in that it looks like it cuts at 45 degrees on the right angle, but this is not the case. If you followed the circle around to point N, then you can no longer see point G.

The problem does not state that you can go higher in height,

Hope that helps, thanks.

 

[Nathanael]

I am trying to find theta.

Am I correct in assuming that the problem is asking for the MAXIMUM theta in which you can still see point G?

It is not really perfectly drawn in that it looks like it cuts at 45 degrees on the right angle, but this is not the case.

This isn't what I meant when I said the drawing is incorrect.

If you followed the circle around to point N, then you can no longer see point G.

Yes, I understand that you can't go all the way up to point N... But you CAN go up higher than point O

The problem does not state that you can go higher in height,

When I said "higher" I meant "higher on the circle" or in other words "you can go to a larger angle"

This is at point O on the diagram.

My whole point is that this (the largest theta where you can still see point G) is NOT at point O

 

[lubo]

from Nathanael, Am I correct in assuming that the problem is asking for the MAXIMUM theta in which you can still see point G?

Yes you are correct.

From Nathanael, Yes, I understand that you can't go all the way up to point N... But you CAN go up higher than point O

Yes that is correct.

From Nathanael, My whole point is that this (the largest theta where you can still see point G) is NOT at point O

Yes you are correct. I am trying to find the largest theta where the point G can still be visible on the circle with the data given. What is this angle or the best way to find it please?

Thanks

 

[NascentOxygen]

Point G can be visible by constructing a right angled triangle B O G and you should be able to use trigonometry.

Please see attached for the drawing.

You have drawn the diagram incorrectly. Start again, only draw it a little differently this time.

 

[Nathanael]

I am trying to find the largest theta where the point G can still be visible on the circle with the data given. What is this angle or the best way to find it please?

What is special about the highest point on the circle where you can still see point G?

What is unique about it? What sets it apart from all the other (lower) points where you can see G from?

Maybe figuring that out will give you enough information to solve the problem

 

[Nathanael]

Try thinking about it this way:

If I give you a point on a circle, how can you find the lowest point that is visible at that point?

 

[lubo]

Hi,

I appreciate all of your comments and I have tried to redraw the question. I understand what you are telling me about you can see point G from a higher point on the circle. I have drew the diagram to show this more clearly and with all the data I have.

I clearly still do not know how to approach this, but I am looking for the angle θ. I want to calculate the extreme angle that G can be visible from O by constructing the right angled triangle BOG attached (it doesn't look like a right angled triangle to me?). This is pretty much identical to what I have in the question and I could not possible draw it any better.

The question states that I should be able to use trigonometry for this (It does not say I can)?

It then follows that I should then also calculate the distance of the (line OG) without using the result from the previous part of the question (just for information at this time).

r = 6000 km
R = 42000 km

Please see attached drawing. Hopefully this will bring about a few more suggestions rather than problems about my explanation attempts.

 

[NascentOxygen]

I see a triangle. It should be a right-angle triangle.
All that remains now is for you to mark in the right-angle. ☺☹


Is that a tangent you've drawn?

 

[lubo]

If I use the triangles N - B - O:

Cos θ = adjacent/hypotenuse = 6000 (radius (r)) /6000 (Radius (r))

θ = (arccos(1)) = 0°

Surely this cannot be true? If I have found this angle correctly then I can use this by taking 90 - answer = my Theta for the highest point to see.

As mentioned I could use Cosine rule but the question suggests this to be done using a right angle triangle? I know this will change later as you move lower on the circle to see point G, but at this time this is all I can see in relation to the problem and right angled triangles.

 

[NascentOxygen]

You are told that BOG is a right-angled triangle. It appears to be, the way you last drew it. So can you mark in the right-angle at O.