- #1
nmnna
- 22
- 3
- Homework Statement
- In figure
- Relevant Equations
The Figure
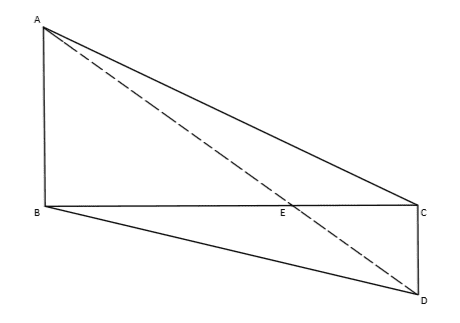
My Attempt at Solution
Similarly
After this I checked the answer in my textbook, and instead of 6.43cm the answer for
I thought that there was a typo in the problem, so instead of
So I'd like to know if it really is a typo or my solution is wrong.
And I can't find the angle required in the problem, so I'd be grateful if you give me some hints for finding this angle.
My Attempt at Solution
Similarly
After this I checked the answer in my textbook, and instead of 6.43cm the answer for
I thought that there was a typo in the problem, so instead of
So I'd like to know if it really is a typo or my solution is wrong.
And I can't find the angle required in the problem, so I'd be grateful if you give me some hints for finding this angle.