What is the angle of displacement from the vertical for a hanging mass on Earth?

[rbwang1225]

Homework Statement

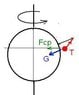
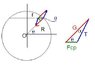
Find an expression for the angle of displacement from the vertical with which a mass hangs in the gravitational field of the Earth as a function of latitude λ.

Homework Equations

The Attempt at a Solution

I don't even understand what the question is, can someone explain it to me?

 

[technician]

I don't understand this question ! I thought that vertical was the direction of a hanging mass.
Have you got any more information or a context for the question

 

[ehild]

The Earth rotates, so all objects go around a circle of radius which corresponds to the latitude in a plane perpendicular to the axis of Earth. Gravity G acts vertically pointing to the centre of Earth, but there should be a force component to ensure the centripetal force needed for the circular motion, and this force Fcp is perpendicular to the rotation axis of Earth. The other force exerted on the object is the tension T of the string: the resultant of T and G is the centripetal force Fcp.
Draw the triangle of the forces, and find relation between its angles and the angle of latitude.
Find the radius of the circle the object moves. You also need the angular velocity. ehild

 

[ehild]

I don't understand this question ! I thought that vertical was the direction of a hanging mass.
Have you got any more information or a context for the question

The vertical is the direction towards the Earth's centre.

ehild

 

[technician]

I see what it means now
Thanks ehild

 

[ehild]

Vertical is matter of definition, you can define it as that of a hanging mass, but then it is influenced by the inhomogeneities of the crust. It is deflected in the direction of a heavy metallic bulk under surface and away from a cavity filled with gas. The direction towards the centre of Earth is at least well defined. ehild

 

[ehild]

Some more hints: There is the triangle of forces, gravity (G) tension (T) and centripetal force (Fcp). The angle between Fcp and G is equal to the latitude. You need to find the angle α the string encloses with the direction of G. The magnitude of G is mg, Fcp can be calculated, and the angles are obtained by applying the Cosine Law and Sine Law.

ehild

 

[rbwang1225]

I've got this relation:

Cos$\alpha$=$\frac{mg^{2}+(\frac{mv^{2}Sinλ}{rSin\alpha})^{2}-(\frac{mv^{2}}{r})^{2}}{2mg\frac{mv^{2}Sinλ}{rSin \alpha}}$

It seems that this expression can't be reduced to be a simple form, am I right?

 

[rbwang1225]

where v is the velocity of the mass and it can be derived by considering the rotation of the Earth.

 

[ehild]

The question is the numerical value of alpha, you need to calculate it.

I do not understand your formula, how did you get it? And it contains the unknown alpha on both sides. It has to be isolated.

ehild

 

[rbwang1225]

$\frac{T}{sin\theta}$ = $\frac{m\frac{v^2}{r}}{sin\alpha}$ $\Rightarrow$ T = $\frac{m\frac{v^2}{r}}{sin\alpha}$$sin\theta$

cos$\alpha$ = $\frac{mg^2+T^2-(m\frac{v^2}{r})^2}{2mgT}$

Then I got the above result.

 

[ehild]

I see. But you have to isolate and calculate alpha.

You will get the numerical value of sin(alpha) if you calculate T with the Law of Cosines first, and then apply the Sine Law.

There is a simpler derivation, using only the Sine Law.

The third angle of the triangle with sides Fcp, T and G, opposite to G is γ=(180-α-θ). According to the Sine Law, $$\frac{\sin(\alpha)}{sin(180-(\alpha+\theta))}=\frac{F_{cp}}{G}$$

As sin(180-angle)=sin(angle) for all angles,

$$\frac{\sin(\alpha)}{sin(\alpha+\theta)}=\frac{F_{cp}}{G}$$

If you calculate Fcp you will see that Fcp << mg. Therefore sinα must be very small, which means alpha very small with respect to theta. You can approximate the denominator by sinθ. So the sine of the angle of deflection is

$$\sin(\alpha)=\sin(\theta)\frac{F_{cp}}{G}=\frac{R\sin(\theta)\cos(\theta)\omega^2}{g}$$
where R is the radius of Earth, θ is the latitude, ω is the angular speed of rotation of Earth and g equals to the gravitational acceleration on the surface of Earth, at R distance from the centre (g≈9.8 m/s²). Substituting all data, alpha is about 0.1°.

ehild