- #1
anemone
Gold Member
MHB
POTW Director
- 3,883
- 115
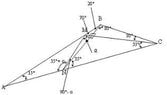
In the triangle ABC, we have $\angle ABC=100^\circ$, $\angle ACB=65^\circ$, $M\in AB$, $N\in AC$, $\angle MCB=55^\circ$ and $\angle NBC=80^\circ$. Find $\angle NMC$.